江苏地区高一数学下学期向量的加法 新课标 人教必修版 课件VIP免费

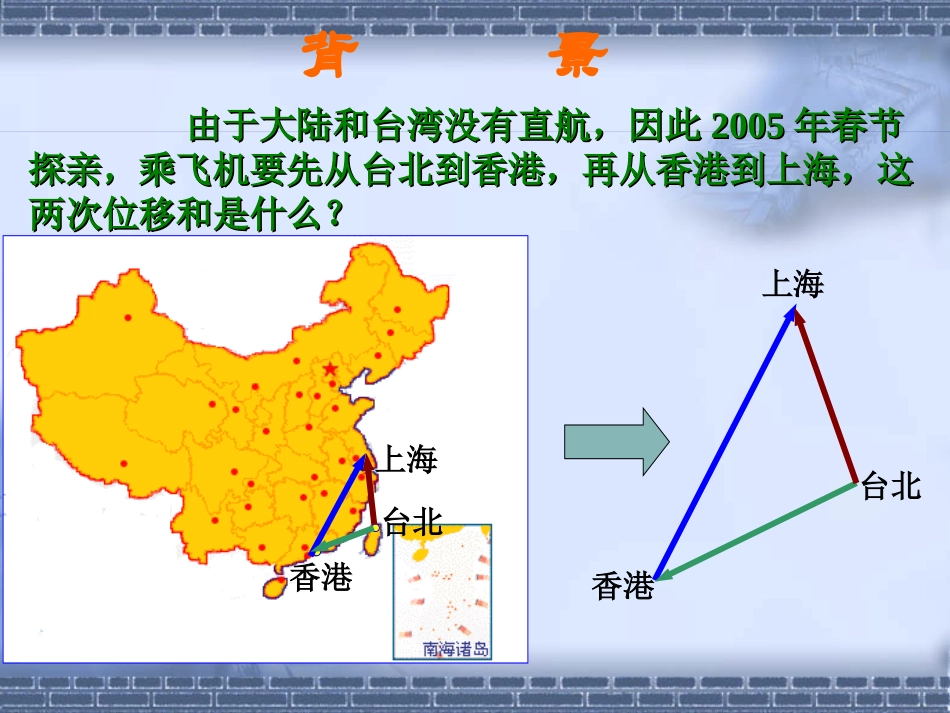
向量的加法向量的加法向量的加法向量的加法背景由于大陆和台湾没有直航，因此由于大陆和台湾没有直航，因此20052005年春节年春节探亲，乘飞机要先从台北到香港，再从香港到上海，这探亲，乘飞机要先从台北到香港，再从香港到上海，这两次位移和是什么？两次位移和是什么？上海台北香港上海台北香港背景物理上有力的合成，速度的合成这些物理上有力的合成，速度的合成这些都是向量加法的背景。都是向量加法的背景。例如:表示，用一人向东走akm,3表示，，用再向北走bkm4为那么这个人的位移之和km5向东北走了ba记为abba经过两次位移后游艇的合位移是多少?想一想：想一想：湖面上有三个景点O,A,B,一游艇将游客从景点O送至景点A,半小时后，游艇再将游客送至景点B.从景点O到景点A有一个位移，从景点A到景点B也有一个位移,那么经过两次位移后游艇的合位移是多少呢?OAABoBAABOA，，OB向量的加法：向量的加法：求两个向量和的运算叫记为的和和叫做则向量再作作在平面上任取一点和已知向量.,,,,,babaOBbABaOAOba向量的加法向量的加法..向量的加法向量的加法..baOBba+b根据向量加法的定义得出的求向量和的方根据向量加法的定义得出的求向量和的方法法,,称为称为向量加法的三角形法则向量加法的三角形法则aA两种特例abABC方向相同CAB方向相反baACbaACab零向量与任一向量,有aaaa00对于相反向量，有0aaaa）（）（回顾反思：b.a),ba求作向量（如图、已知向量AaaabbbbbbabOaBba+bb.aOB,bAB,aOAO,:＝则作在平面内任取一点作法首尾顺次相连练习ba如图,已知用向量加法的三角形法则作出ba,abba（1）（2）（3）abba（4）abbaabbbabbba向量加法的平行四边形法则向量加法的平行四边形法则baAaaaaaaaabbbBbaDaCba+b对于两个不共线的非零向量,我们还可以作平行四边形来求两个向量的和.分别作，，以为邻边作平行四边形，则以为起点的对角线就是向量与的和,我们把这种方法叫做OCOA,OABCOba,aOAbOCOBab向量加法的平行四边形法则向量加法的平行四边形法则练习如图,已知用向量加法的平行四边形法则作出baba,（1）abbbaababa（2）共起点向量加法的运算律向量加法的运算律交换律：交换律：abba结合律：结合律：)()(cbacbabacbaabcabccbacb如果平面内有n个向量依次首尾相连组成一条封闭折线，那么这n个向量的和是什么？思考：数学应用1(2)(3)OABCDEFOAOCBCFEOAFE�例1：已知为正六边形的中心，作出下列向量（）;1OBOCOA）解：（;2ADFEBC）（.03FEOA）（ABCDEFO定船的航向。要垂直度过长江，请确渡船度为的速度东流，渡船的速水以：在长江某岸某处，江例,/25/5.122hkmhkmC解解：如图，设表示水流的速度，表示渡船的速度，ABAD表示渡船实际垂直过江的速度.AC因为，所以四边形为平行四边形.在中，ACADABABCDACDRt90ACD5.12||||ABDC25||AD所以30CAD答：要垂直地度过长江，其航向应为北偏西3025D5.12BA当堂反馈：课本P63页练习1，2,3)4()3()2()1(edcdbadcba１.化简________)1(BCCDAB________)2(CBACBNMA________)3(DCCABDAB２.根据图示填空abcdefgABDECcfgfADMN0３.一架飞机向西飞行,然后改变方向向南飞行,则飞机两次位移的和为.km100km100km210045，西偏南北南西东km100ABkm100C450km2100BCABAC目标检测课堂小结：向量加法的定义向量加法的运算律三角形法则平行四边形法则向量加法的运算作业布置:课本P63:4P68;1