高一数学(一元二次不等式及其解法(2))课件VIP免费

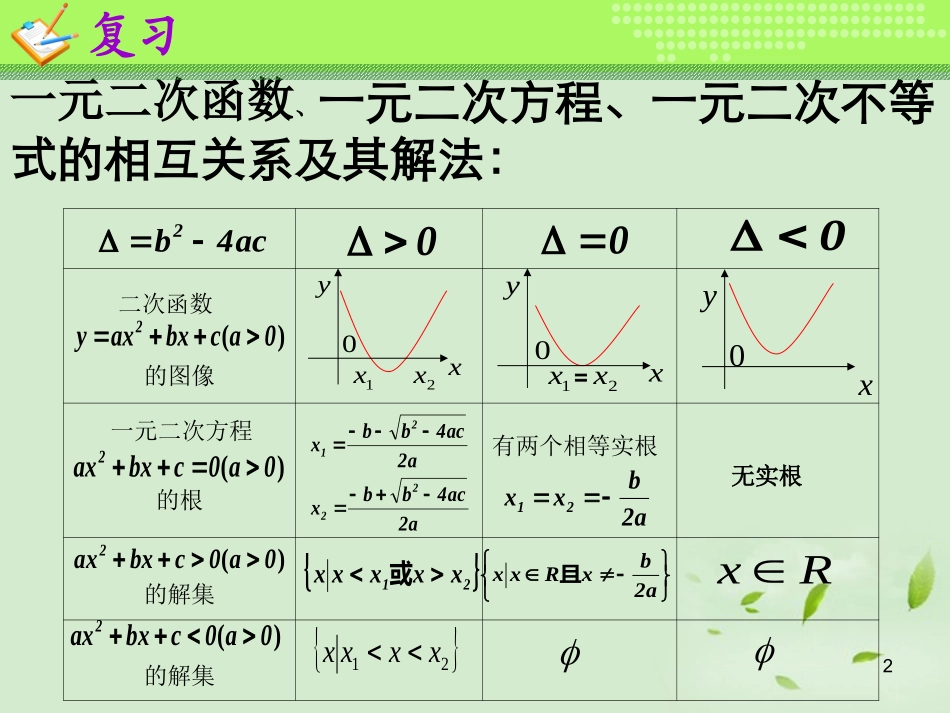
1一元二次不等式及其解法(二)2一元二次函数、一元二次方程、一元二次不等式的相互关系及其解法：的图像的根的解集的解集ac4b2000二次函数)(0acbxaxy2一元二次方程)(0a0cbxax2)(0a0cbxax2)(0a0cbxax21x2xyx0xy01x2x=xy0有两个相等实根a2ac4bbxa2ac4bbx2221a2bxx2121xxxxx或21xxxxRxa2bxRxx且无实根复习3解一元二次不等式的一般步骤1：确定二次项系数符号（一般将二次系数化为正）2：判别△（能十字相乘法的不需判别）3：用求根公式得出一元二次方程的两根（能用十字相乘法的不需用公式）4：由1、2、3三个步骤画出不等式所对应函数的大致图像5：根据所画图像得出不等式的解集复习4例1.求不等式的解集.例题讲解)2xx(log)2x5x2(log：2222变2xx2x5x222)21()21)(4(02x5x2)1(245x2x3)2(03xlog2xlog)3(222}2x2222x2|x{或}1x0|x{}21x0|x{8x或}6x|x{0x或}221x0|x{6x或5例1.求不等式的解集.例题讲解)2xx(log)2x5x2(log：2222变2xx2x5x222)21()21)(4(02x5x2)1(245x2x3)2(03xlog2xlog)3(222•注意：不是一元二次不等式，但可以通过换元、利用函数性质化归为解一元二次等式问题；在化归时应注意变元的范围、以及函数的定义域对不等式的解集的影响.6对二次项系数进行讨论.mx01mxmx)x(f、22的取值范围恒成立，求实数对于一切实数设函数例例题讲解0mx2xx32的不等式解关于例对所对应方程根的个数进行讨论对所对应方程根的大小进行讨论0ax)aa(xx、4322的不等式解关于例702x)1a2(axx52的不等式：：解关于例综合题型1例题讲解0ax2axx62的不等式：解关于例综合题型2•注意：因不确定所以需要讨论，在讨论时需清楚在哪讨论；怎样讨论.讨论要不重不漏,通过讨论后化不确定为确定.82、含参数的一元二次不等式需讨论一般分为1)对二次项系数进行讨论；2)对所对应方程根的个数进行讨论；3)对所对应方程根的大小进行讨论；小结1、化归为一元二次不等式常用方法1)换元法；2)函数性质法；901x)1a(axx、42的不等式解关于.mx03x)1m(4x)5m4m(、222的取值范围恒成立，求实数对于一切实数已知不等式0m1x2xx、322的不等式解关于作业.，0)，R、1的取值范围求实数且在其定义域内递减上的奇函数定义在aa-a-f(1a)-f(2f(x)2