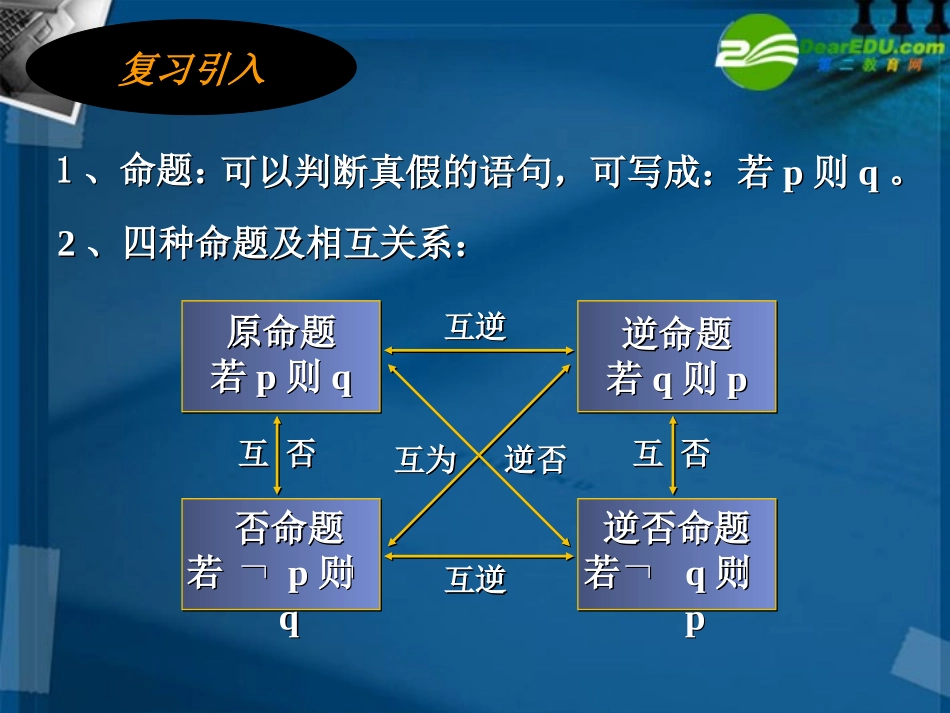
1、命题:1、命题:可以判断真假的语句,可写成:若p则q。可以判断真假的语句,可写成:若p则q。2、四种命题及相互关系:2、四种命题及相互关系:逆命题若q则p逆命题若q则p原命题若p则q原命题若p则q否命题若p则q否命题若p则q逆否命题若q则p逆否命题若q则p互逆互逆互逆互逆互否互否互否互否互为逆否互为逆否复习引入课堂练习1.判断下列说法是否正确。1)一个命题的逆命题为真,它的逆否命题不一定为真;(对)2)一个命题的否命题为真,它的逆命题一定为真。(对)3)一个命题的原命题为假,它的逆命题一定为假。(错)4)一个命题的逆否命题为假,它的否命题为假。(错)2:设原命题是:当c>0时,若a>b,则ac>bc.写出它的逆命题、否命题、逆否命题。并分别判断它们的真假。解:逆命题:当c>0时,若ac>bc,则a>b.否命题:当c>0时,若a≤b,则ac≤bc.逆否命题:当c>0时,若ac≤bc,则a≤b.(真)(真)(真)分析:“当c>0时”是大前提,写其它命题时应该保留。原命题的条件是“a>b”,结论是“ac>bc”。3若m≤0或n≤0,则m+n≤0。写出其逆命题、否命题、逆否命题,并分别指出其真假。分析:搞清四种命题的定义及其关系,注意“且”“或”的否定为“或”“且”。解:逆命题:若m+n≤0,则m≤0或n≤0。否命题:若m>0且n>0,则m+n>0.逆否命题:若m+n>0,则m>0且n>0.(真)(真)(假)小结:在判断四种命题的真假时,只需判断两种命题的真假。因为逆命题与否命题真假等价,逆否命题与原命题真假等价。思考:判断下列命题的真假:(1)若x>a2+b2,则x>2ab;(2)若a>b>0,则a2>b2;(3)若ac>bc,则a>b;(4)若ab=0,则a=0;真真假假一般地,“若p则q”是真命题,则说明pq“若p则q”是假命题,则说明pq¿思考:对命题“若x>a2+b2,则x>2ab”,下列说法是否正确?(1)要使“x>2ab”,只要“x>a2+b2”就够了;(2)若“x>a2+b2”要成立,则“x>2ab”一定要成立.(1)因为“x>a2+b2”成立就足以推出“x>2ab”成立所以我们说,“x>a2+b2”是“x>2ab”成立的充分条件(2)因为“x>2ab”是“x>a2+b2”成立必不可少的条件所以我们说,“x>2ab”是“x>a2+b2”成立的必要条件一般地,对于命题“若p,则q”为真命题,即pq则我们说,p是q的充分条件,q是p的必要条件注意:(1)“p是q的充分条件”意味着:p成立就足以推出q成立(2)“q是p的必要条件”意味着:若p要成立则q必不可少(3)对同一个真命题“若p,则q”,有_____;_____;ABABABAB练习:用、、、填空(1)若为的充分条件,则(2)若为的必要条件,则¿¾“p是q的充分条件”“q是p的必要条件”判断充分条件和必要条件的方法:ABABBA“”“是的充分条件”“是的必要条件”ABABBA“”“是的必要条件”“是的充分条件”pq,相当于pq,即pq,相当于pq,即从集合角度理解:从集合角度理解:从集合角度理解:从集合角度理解:•P足以导致q,也就是说条件p充分了;•q是p成立所必须具备的前提。充分条件与必要条件的理解pq1、从概念的角度理解(1),pqpq若则是的充分条件;(2),qppq若则是的必要条件;2、从命题的角度去理解设原命题为“若p,则q”如果原命题为真,则p是q的充分条件如果逆命题为真,则p是q的必要条件3、从集合的角度去理解若p以集合A的形式出现,q以集合B的形式出现AxpxBxqx即(),()ABpq若,则是的充分条件BApq若,则是的必要条件判断方法:例1、下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件?(1)若x=1,则x2-4x+3=0;(2)若f(x)=x,则f(x)为增函数;(3)若x为无理数,则x2为无理数.解:命题(1)(2)是真命题,命题(3)是假命题.所以,命题(1)(2)中的p是q的充分条件.例2、下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件?(1)若x=y,则x2=y2;(2)若两个三角形全等,则这两个三角形的面积相等;(3)若a>b,则ac>bc.解:命题(1)(2)是真命题,命题(3)是假命题.即p能推出q.所以,命题(1)(2)中的q是p的必要条件.例3、判断下列命题中前者是后者的什么条件?后者是前者的什么条件?(1)若a>b,c>d,则a+c>b+d。(2)ax2+ax+1>0的解集为R,则0
b2,则a>b。例3、判断下列命题...