高中数学：13(函数的最值与导数)课件(新人教A版选修2-2) 课件VIP免费

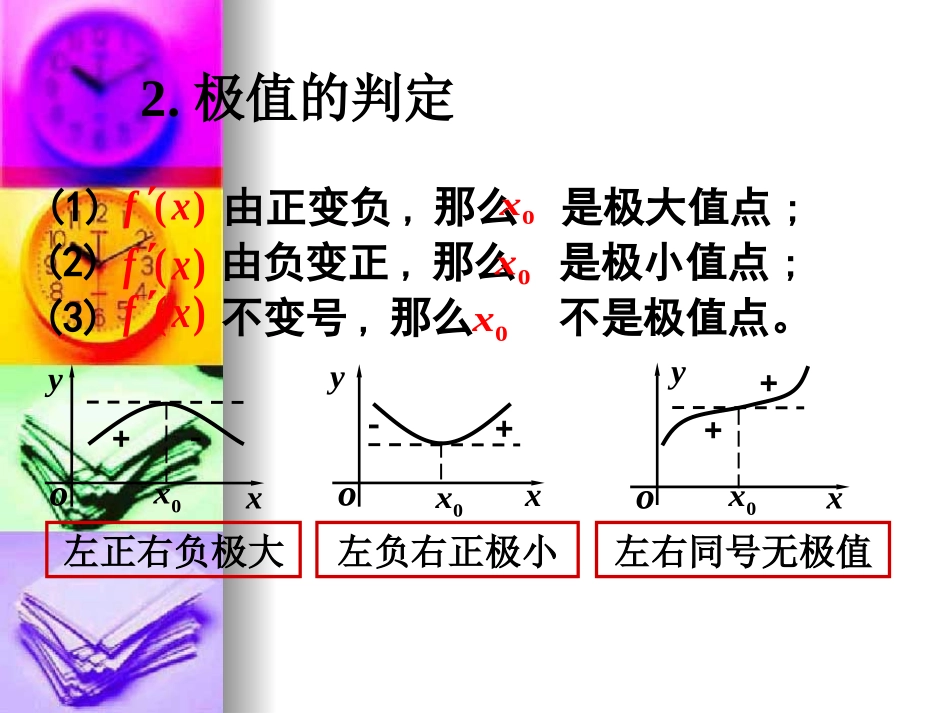
函数的最值与导数(1)()0fx()为单调递增函数fx(2)()0fx()为单调递减函数fx0(3)为极值点x0()0fx1、导数与单调性的关系复习xyo0x左正右负极大左负右正极小左右同号无极值(2)由负变正,那么是极小值点;0x()fx(3)不变号,那么不是极值点。0x()fx(1)由正变负,那么是极大值点;()fx0x2.极值的判定yxo0xxoy0x(1)求导函数fˊ(x)；(2)求解方程fˊ(x)=0；(3)检查fˊ(x)在方程fˊ(x)=0的根的左右的符号，并根据符号确定极大值与极小值.口诀：左负右正为极小，左正右负为极大.用导数法求解函数极值的步骤：复习求函数最值1)在某些问题中，往往关心的是函数在整个定义域区间上，哪个值最大或最小的问题这就是我们通常所说的最值问题.2)在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.xy0abx1x2x3x4f(a)f(x3)f(b)f(x1)f(x2)gg新课oxyaboxyaboyoxyaby=f(x)y=f(x)y=f(x)xaby=f(x)归纳结论：（1）函数f（x）的图像若在开区间（a，b）上是连续不断的曲线，则函数f（x）在（a，b）上不一定有最大值或最小值；函数在半开半闭区间上的最值亦是如此（2）函数f（x）若在闭区间[a，b]上有定义，但有间断点，则函数f（x）也不一定有最大值或最小值总结：一般地，如果在区间[a，b]上函数f（x）的图像是一条连续不断的曲线，那么它必有最大值和最小值。如何求最值？只要把连续函数的所有极值与端点的函数值进行比较，就可求最大值、最小值解:24yx当变化时,的变化情况如下表:,yy例1、求函数在区间上的最大值与最小值。31443yxx[0,3]令,解得0y22或xxx又由于(0)4,(3)1ff（舍去）2－－＋＋0(0,2)(2,3)x()fx()fx03↗↗↘↘43极小值41应用函数在区间上最大值为,最小值为43[0,3]4例2：已知函数(1)求的单调减区间(2)若在区间上的最大值为,求该区间上的最小值32()39,fxxxxa()fx()fx[2,2]20所以函数的单调减区间为(,1)(3,)，解:2(1)()369fxxx()0令fx23690即xx13解得:或xx应用2(2)()369fxxx令解得()0fx13或xx当变化时,的变化情况如下表:,yyx（舍去）↘↘----↗↗x()fx()fx(2,1)1(1,2)205a2极小值2a22a2220a2即a最小值为527所以函数的最大值为,最小值为(2)22fa5a(2)将y=f(x)的各极值与f(a)、f(b)(端点处)比较,其中最大的一个为最大值，最小的一个最小值.求f(x)在闭区间[a,b]上的最值的步骤(1)求f(x)在区间(a,b)内极值(极大值或极小值)小结解:2(1)()33fxx令解得()0fx11或xx所以函数的极大值为，极小值为1、已知函数(1)求的极值(2)当在什么范围内取值时，曲线与轴总有交点3()3,[2,3]fxxxax()fxxa()yfx2a2a当变化时,的变化情况如下表:(),()fxfxx↘↘----++↗↗↘↘x()fx()fx(2,1)1(1,1)1(1,3)0----2a2a0极小值极大值练习218即a2a18a曲线与轴总有交点x()yfx20180aa由（1）可知，函数在区间上的极大值为，极小值为，又因，2a(2)2fa(3)18fa[2,3]2a(2)所以函数的最大值为，最小值为2、求函数f(x)=3x-x3在区间[-3，3]内的最大值和最小值.练习一.是利用函数性质二.是利用不等式三.是利用导数注：求函数最值的一般方法课本32页第6题(1)(2)(3)课后作业