高中数学 25等比数列的前n项和1课件 新人教A版必修5 课件VIP免费

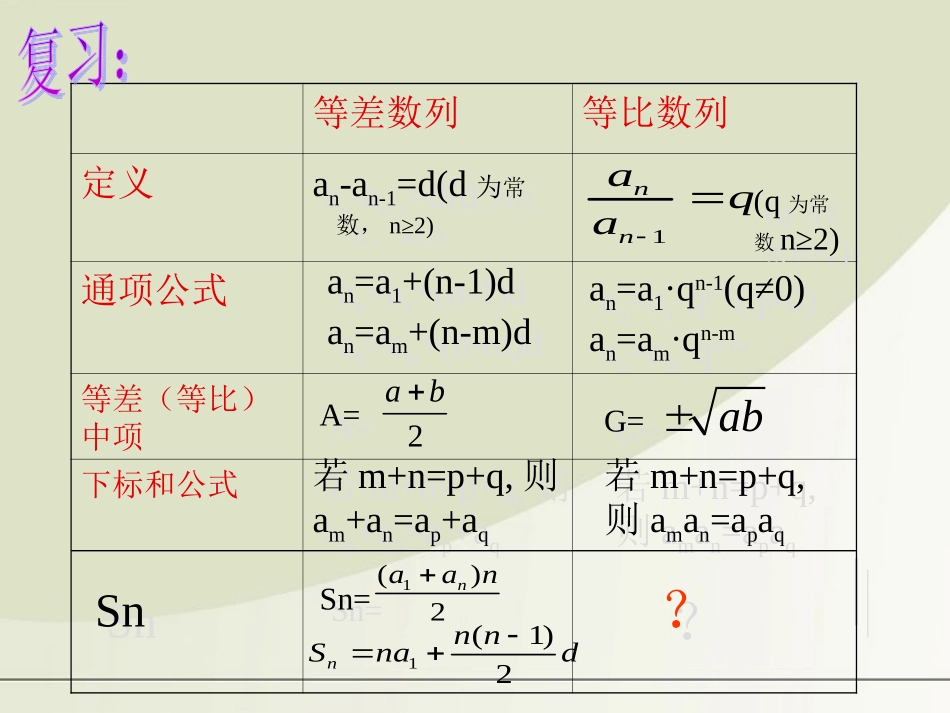
§2.5§2.5等比数列的前等比数列的前nn项和项和((一一))等差数列等比数列定义通项公式等差（等比）中项下标和公式2abab1nnaqaSnSnSn=Sn=1()2naan1(1)2nnnSnad？？an-an-1=d(d为常数，n≥2)an-an-1=d(d为常数，n≥2)(q为常数n≥2)(q为常数n≥2)an=a1+(n-1)dan=am+(n-m)dan=a1+(n-1)dan=am+(n-m)dan=a1·qn-1(q≠0)an=am·qn-man=a1·qn-1(q≠0)an=am·qn-mA=A=G=G=若m+n=p+q,则am+an=ap+aq若m+n=p+q,则am+an=ap+aq若m+n=p+q,则aman=apaq若m+n=p+q,则aman=apaq引入新课张明和王勇是中学同学，张明学习成绩优异，考上了重点大学。王勇虽然很聪明，但对学习无兴趣，中学毕业后做起了生意，凭着机遇和才智，几年后成了大款。一天，已在读博士的张明遇到了王勇，寒暄后王勇流露出对张明清苦的不屑。表示要资助张明，张明说：“好吧，你只要在一个月30天内，第一天给我1分钱，第二天给我2分钱，第三天给我4分钱，第四天给我8分钱，依此类推，每天给我的钱都是前一天的2倍，直到第30天。”王勇听了，立刻答应下来心想:这太简单了。没想到不到30天，王勇就后悔不迭，不该夸下海口。同学们，你们知道王勇一共应送给张明多少钱吗？拿度甚至全世界的麦粒全王才发现：就是把全印国麦子搬来开始计数时，粒．当人们把一袋袋的麦足了，就命令给他这些王觉得这要求太容易满国赏赐给您的仆人吧！＂所有６４格的麦粒，都上．请您把这样摆满棋盘格都比前一小格加一倍小格里给４粒，以后每一小格里给２粒，第３小个给我１粒麦子，在第２盘的第１个小格里，赏棋：＂陛下，请您在这张想要什么，他对国王说达依尔．国王问他班宰相西萨—象棋的发明人际说：舍罕王打算奖赏国在印度有一个古老的传64S236312222.(1)请同学们考虑如何求出这个和？642S23632(12222).642S即23636422222.(2)64642SS23463(122222)…2346364(222222)646421S这种求和的方法,就是错位相减法!191.841018446744073709551615如果1000粒麦粒重为40克，那么这些麦粒的总质量就是7300多亿吨。根据统计资料显示，全世界小麦的年产量约为6亿吨，就是说全世界都要1000多年才能生产这么多小麦，国王无论如何是不能实现发明者的要求的。少呢？求得到的麦粒到底有多要相的要求．那么，宰相来，也满足不了那位宰等比数列前n项求和公式通项公式:an=a1•qn-1解：Sn=a1+a2+a3+a4+…+anqsn=(1-q)Sn=a1-a1qna1qa1q23…a1qn-1=a1+a1q++++作减法23111111nnaqaqaqaqaq1(1)1nnaqSq注意：此时q≠1注意：此时q≠1若q=1,若q=1,1nSna?,3211nnnaaaaSnqaa即求它的前和，，为等比数列，已知：)1()1(1)1(11qanqqqaSnn)1()1(111qanqqqaaSnn或:8.1项和求下列等比数列的前例;,81,41,21)1(.0,2431,27)2(91qaa解:(1)由,211a,212141qn=8，得2112112188S25625521188272431q＝可得91,2431,272aa由31,0qq可得又由8n时，于是当8116403113112788S:,.1nnSna项和的前求相应的等比数列根据下列各题中的条件练;6,2,3)1(1nqa.901,31,7.2)2(1naqa:3.2kSnannn项和的前已知数列例;)1(求通项公式.,)2(的值求是等比数列若kan.____,3.2则这个数列项和的前已知数列练nnnSna的等比数列是公比为2.A的等比数列是公比为3.C的等比数列项起是公比为第22.B的等比数列项起是公比为第32.D1,1,{,}{111nssnsaasnannnnn则：项和为的前若数列.,,,232成等比数列则项和为的前若等比数列kkkkknnSSSSSSna.____15,5010,105.3项和为那么它的前项和为前项和为一个等比数列的前练.,,:,.314217147成等比数列求证项和为的前已知等比数列例SSSSSSnann小结,111qqannS,1na(q=1).(q≠1).{1.已知则qna,,1,11qqaannS,1na(q=1).(q≠1).{已知则qaan,,12.对含字母的题目一般要分别考虑q=1和q≠1两种情况。填表数列等差数列等比数列前n项和公式推导方法21nnaanSdnnna211qqann111Sqqaan111q【注意】在应用等比数列的前n项和公式时考虑.倒序相加错位相减公比是否为1