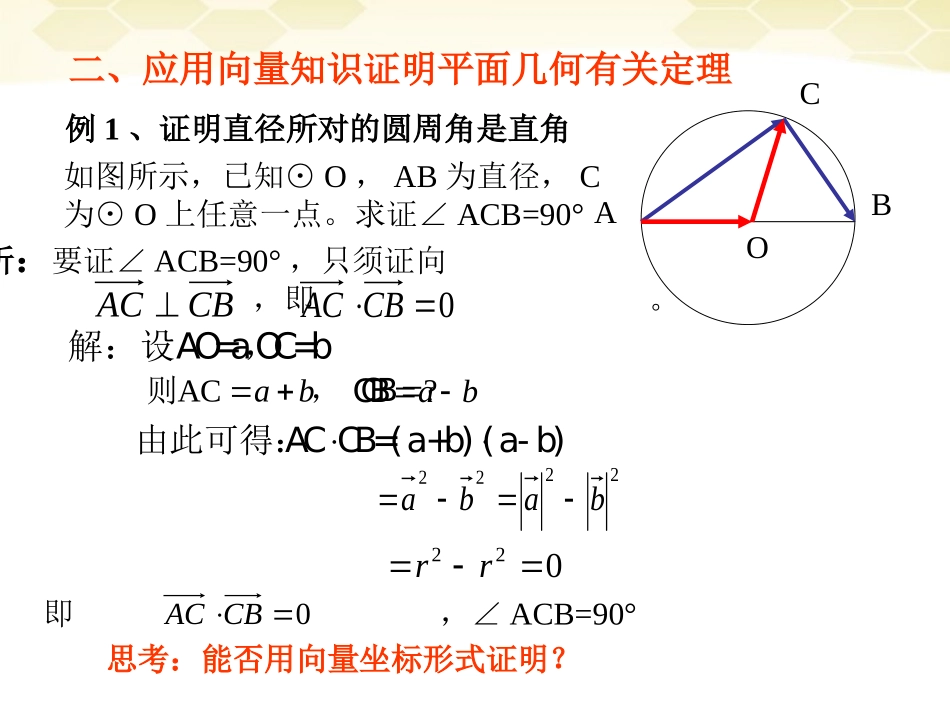
一、向量有关知识复习(1)向量共线的充要条件:ab与共线0,bRba(2)向量垂直的充要条件:0,00bababa(3)两向量相等充要条件:,baba且方向相同。11221221(,)(,)//0axybxyabxyxy,,11221212(,)(,)0axybxyabxxyy,,11221212(,)(,),axybxyabxxyy,,(4)平面向量基本定理1212aeeee,其中,不共线。,为唯一确定的常数二、应用向量知识证明平面几何有关定理例1、证明直径所对的圆周角是直角ABCO如图所示,已知⊙O,AB为直径,C为⊙O上任意一点。求证∠ACB=90°分析:要证∠ACB=90°,只须证向量,即。CBAC0CBAC2222baba022rr即,∠ACB=90°0CBAC思考:能否用向量坐标形式证明?�解:设AO=a,OC=bACab�则,�由此可得:ACCB=(a+b)(a-b)?�CBab�CB二、应用向量知识证明平面几何有关定理例2、证明平行四边形四边平方和等于两对角线平方和ABDC已知:平行四边形ABCD。求证:222222BDACDACDBCABbADaAB,解:设,则baDBbaACaDAbBC;,,分析:因为平行四边形对边平行且相等,故设其它线段对应向量用它们表示。bADaAB,)(2222222baDACDBCAB2222babaBDAC222222222222bababbaabbaa∴222222BDACDACDBCAB三、应用向量知识证明三线共点、三点共线例3、已知:如图AD、BE、CF是△ABC三条高求证:AD、BE、CF交于一点FABCDEABCDEH分析:思路一:设AD与BE交于H,只要证CHAB⊥,即高CF与CH重合,即CF过点H由此可设aBCbCApCH利用ADBC⊥,BECA⊥,对应向量垂直。00)(apabapbBCHA00)(bpabbpaCABH0)(0bapbpapBACHBACH0BACH�只须证明0pBA�如何证?三、应用向量知识证明三线共点、三点共线例3、已知:如图AD、BE、CF是△ABC三条高求证:AD、BE、CF交于一点ABCDEH解:设AD与BE交于H,aBCbCApCH00)(apabapbBCHA00)(bpabbpaCABH0)(0bapbpapBACHBACH0即高CF与CH重合,CF过点H,AD、BE、CF交于一点。三、应用向量知识证明三线共点、三点共线例4、如图已知△ABC两边AB、AC的中点分别为M、N,在BN延长线上取点P,使NP=BN,在CM延长线上取点Q,使MQ=CM。求证:P、A、Q三点共线ABCNMQP解:设bACaAB,则aAMbAN21,21由此可得abNPBN21baMQCM21baabPANPANPA)(,baabAQMQAMAQ)(,AQPA即故有,且它们有公共点A,所以P、A、Q三点共线AQPA//四、应用向量知识证明等式、求值例5、如图ABCD是正方形M是BC的中点,将正方形折起,使点A与M重合,设折痕为EF,若正方形面积为64,求△AEM的面积ABCDMNEF分析:如图建立坐标系,设E(e,0),M(8,4),N是AM的中点,故N(4,2)(8,4)AM�AEANEN=(4,2)-(e,0)=(4-e,2)(8,4)(4,2)0AMENe�解得:e=5故△AEM的面积为10四、应用向量知识证明等式、求值例5、如图ABCD是正方形M是BC的中点,将正方形折起,使点A与M重合,设折痕为EF,若正方形面积为64,求△AEM的面积ABCDMNEF解:如图建立坐标系,设E(e,0),由正方形面积为64,可得边长为8由题意可得M(8,4),N是AM的中点,故N(4,2))4,8(AMAEANEN=(4,2)-(e,0)=(4-e,2)0)2,4()4,8(eENAM解得:e=5即AE=51102AEMSAEBM四、应用向量知识证明等式、求值练习:PQ过△OAB的重心G,且OP=mOA,OQ=nOB求证:311nm分析:由题意OP=mOA,OQ=nOB,联想线段的定比分点,利用向量坐标知识进行求解。OABG·PQ由PO=mOA,QO=nOB可知:OBnQOOAmPO,O分的比为,O分的比为PAQB由此可设由向量定比分点公式,可求P、Q的坐标,而G为重心,其坐标也可求出,进而由向量,得到mn的关系。),()0,(221yxQxPGQPG//-m-n...