高中数学 333点到直线的距离课件1 新人教A版必修2 课件VIP免费

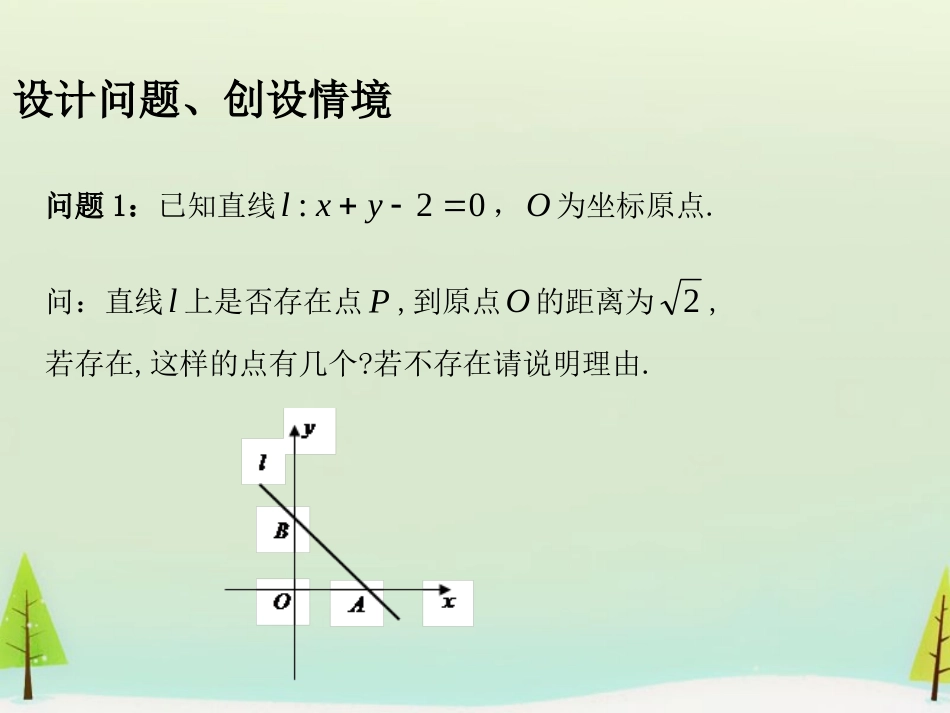
3.3.3点到直线的距离设计问题、创设情境问题1：已知直线02:yxl，O为坐标原点.问：直线l上是否存在点P,到原点O的距离为2,若存在,这样的点有几个?若不存在请说明理由.学生探索、尝试解决思路一、(函数思想)设点),(yxP是直线l上任意一点,则xy2,所以22)1(2442)2(||2222222xxxxxyxOP,所以2||OP.因此,直线l上到原点O的距离为2的点P,仅有一个,即)1,1(P.学生探索、尝试解决思路二、(转化为两点间的距离)直线l的斜率为1,所以过原点且与直线l垂直的直线方程为xy,与02yx联立,解得垂足Q的坐标为)1,1(,所以原点到直线l的距离为2)01()01(22.学生探索、尝试解决思路三、（解三角形）如图，易知045OAQ,在OAQRt中，2||OA，所以2222sin||||OAQOAOQ.思路四、（等面积法）如图，易知2||||OBOA，所以22||AB，2||||||||ABOBOAOQ.信息交流、揭示规律问题2:通过问题1,我们知道点在直线外时,可以用点到直线的距离定量的刻画点与直线的位置关系.你能将这个问题推广到一般情形,得到点到直线的距离公式吗?大家自己提出问题,并制定解决思路或方案.求点),(000yxP到直线0:CByAxl距离.信息交流、揭示规律思路一（函数思想）步骤：①设出直线l上任意一点Q的坐标；②用两点间距离公式表示||PQ，并借助直线方程消元；③将||PQ关于横坐标x的二次函数后求最值.思路二（转化为两点间距离）的步骤：①确定直线l的斜率0kk;②求与l垂直的直线l的斜率1kk;③求过点P垂直于l的直线l的方程;④求l与l的交点Q;⑤求点P与点Q的距离，得到点P到l的距离dPQ.信息交流、揭示规律思路三(解三角形)的步骤:①过点0P作x轴，y轴的垂线交l于点R，S；②用00,yx表示点R，S的坐标；③求出|||,|00SPRP;④利用勾股定理求出||RS,并计算||||sin00RSRPSRP；⑤解三角形SQP0得SRPSPQP000sin||||.信息交流、揭示规律思路四(等面积法)的步骤:①过点0P作x轴，y轴的垂线交l于点R，S；②用00,yx表示点R，S的坐标；③求出|||,|00SPRP;④利用勾股定理求出||RS；⑤根据面积相等，求出||||||||000RSSPRPQP.运用规律、解决问题例题1.求点)2,1(0P到下列直线的距离:(1)xy210;(2)23x解:(1)先将方程xy210化为一般式为0102yx，由点到直线的距离公式得5212|102)1(2|22d.（2）3503|2)1(3|22d.运用规律、解决问题问题4:在公式的推导过程中,BA,可以为零吗?我们得到的点到直线的距离公式中BA,是否可以为零?例2.已知点)0,1(),1,3(),3,1(CBA,求△ABC的面积.解:设AB边上的高为h,则hABSABC||21.22)31()13(||22AB.AB边上的高h就是点C到AB的距离.AB边所在的直线方程为131313xy,即04yx.点)0,1(C到04yx的距离2511|401|22h.因此,5252221ABCS.变练演编、深化提高例题3.已知直线0872:1yxl,01216:2yxl,1l与2l是否平行?若平行,求1l与2l间的距离.解:1l的斜率721k,2l的斜率722162k.1l的纵截距781b,2l的纵截距2112k.因为2121,bbkk,所以21ll.求得1l与x的交点A的坐标为)0,4(.点A到直线2l的距离5315923216102146|22d.所以1l与2l间的距离5315923.变练演编、深化提高问题5:如何求两平行线之间的距离?为什么?你能解决下面的问题吗?求两条平行直线0:11CByAxl和0:22CByAxl之间的距离.当0A时,求得1l与x的交点A的坐标为)0,(AC.点A到直线2l的距离22122221|||0|BACCBACBAACd.当0A是,经验证上述公式也成立.信息交流、教学相长问题6:点到直线的距离公式以及两条平行直线之间的距离公式的推导过程体现出了怎样的数学思想方法?