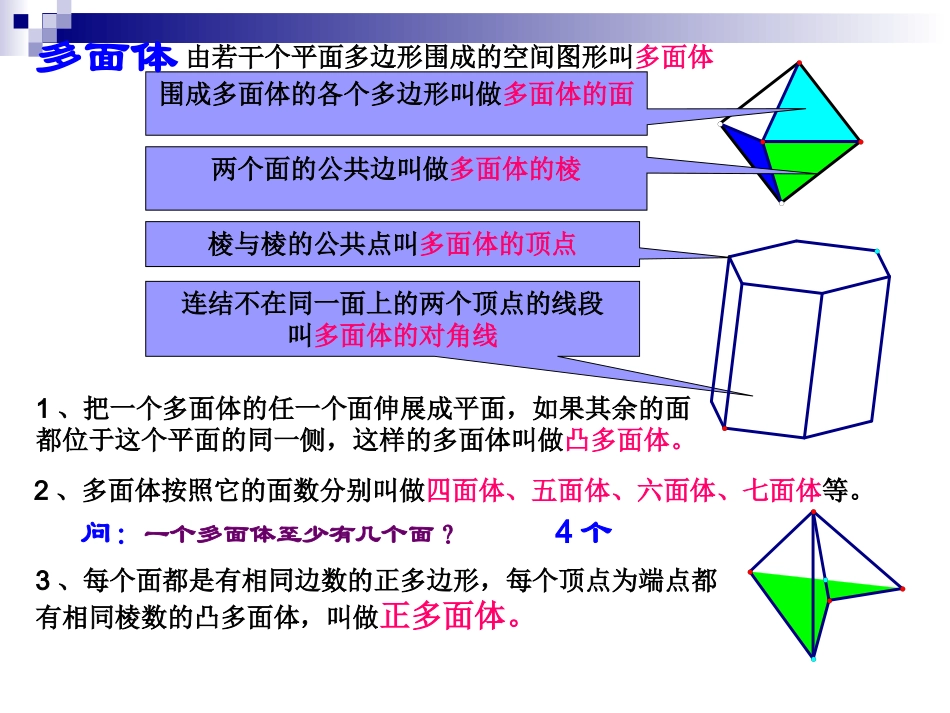
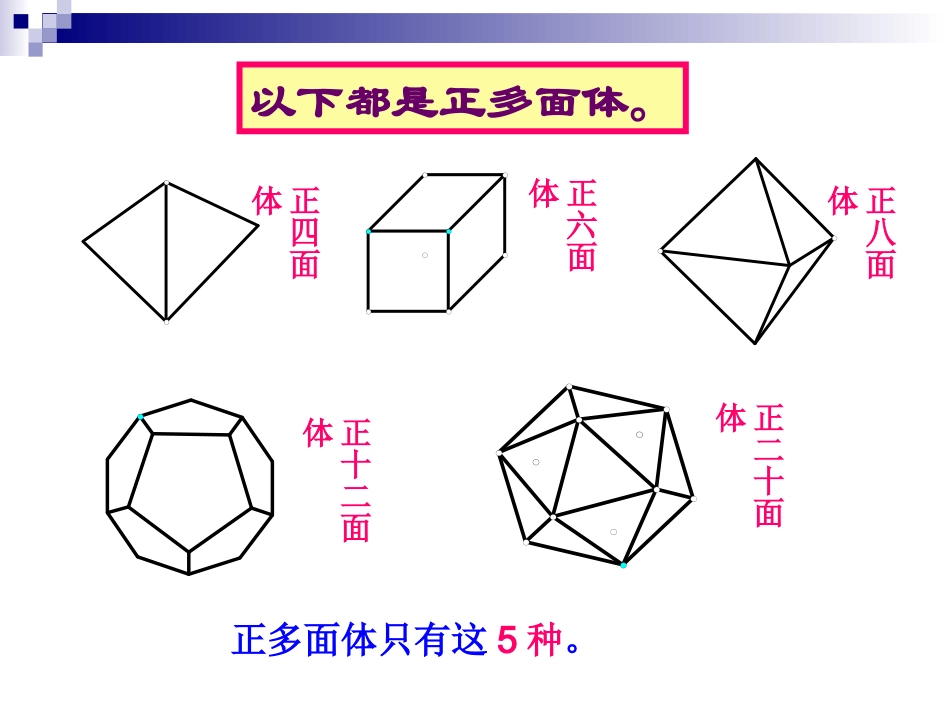
观察下列空间几何图形:这些几何图形都是多面体由若干个平面多边形围成的空间图形叫多面体围成多面体的各个多边形叫做多面体的面两个面的公共边叫做多面体的棱连结不在同一面上的两个顶点的线段叫多面体的对角线多面体1、把一个多面体的任一个面伸展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫做凸多面体。2、多面体按照它的面数分别叫做四面体、五面体、六面体、七面体等。问:一个多面体至少有几个面?3、每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体。4个棱与棱的公共点叫多面体的顶点以下都是正多面体。正四面体正六面体正八面体正十二面体正二十面体正多面体只有这5种。看下列多面体有何特点?如果一个多面体有两个面互相平行,而其余每相邻两个面的交线互相平行,这样的多面体叫做棱柱。棱柱的概念棱柱的概念ABCDEA’B’C’D’E’·H’H·底底两个互相平行的面叫做棱柱的底两个侧面的公共边叫做棱柱的侧棱不在同一个不在同一个面上的两个顶点面上的两个顶点的连线叫做棱柱的连线叫做棱柱的的对角线对角线·H’H··H’H··H’H··H’H··H’H··H’H··H’H··H’H·两个底面两个底面的公垂线段叫的公垂线段叫做棱柱的高做棱柱的高·H’H·其余各面叫做其余各面叫做棱柱的棱柱的侧面侧面底面对角线高侧面侧棱顶点2.用表示一条对角线端点的两个字母表示,如图:记作棱柱AC1A1B1C1D1E1ABCDE棱柱的表示法棱柱的表示法1.用平行的两底面多边形的字母表示棱柱,如图:记作棱柱ABCDE-A1B1C1D1E1棱柱的分类棱柱的分类ABCDEA’B’C’D’E’(1)侧棱不垂直于底面的棱柱叫做斜棱柱按侧棱与底面的关系分(2)侧棱垂直于底面的棱柱叫做直棱柱(3)底面是正多边形的直棱柱叫做正棱柱棱柱的底面可以是三角形、四边形、五边形、……把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、……三棱柱四棱柱五棱柱棱柱的分类棱柱的分类按底面的形状分:性质1.侧棱都相等,侧面是平行四边形;棱柱的性质性质2.两个底面与平行于底面的截面是全等的多边形;性质3.过不相邻的两条侧棱的截面是平行四边形1.斜棱柱、直棱柱的底面为任意多边形。正棱柱的底面为正多边形。思考题1、斜棱柱、直棱柱和正棱柱的底面、侧面各有什么特点?2.斜棱柱的侧面为平行四边形。直棱柱的侧面为矩形。正棱柱的各个侧面为全等的矩形。斜三棱柱直四棱柱正五棱柱思考题21、侧棱不垂直于底面且底面为三角形的棱柱叫做___________;2、侧棱垂直于底面且底面为四边形的棱柱叫做____________;3、侧棱垂直于底面且底面为正五边形的棱柱叫做____________。思考题3棱柱集合、斜棱柱集合、直棱柱集合、正棱柱集合之间存在怎样的包含关系?斜棱柱直棱柱正棱柱棱柱思考题4:下列命题之中的假命题是()A、直棱柱的侧棱是直棱柱的高。B、有一个侧面是矩形的棱柱是直棱柱。C、直棱柱的侧面是矩形。D、有一条侧棱垂直与底面的棱柱是直棱柱。B常见的四棱柱常见的四棱柱平行六面体直平行六面体长方体正方体侧棱与底面垂直底面是矩形棱长都相等例1、证明定理:长方体的对角线的长的平方等于一个顶点上三条棱的长的平方和。CDBC1AB1A1D1例2:已知正三棱柱ABC—A’B’C’的各棱长都为1,M是底面上BC边的中点,N是侧棱CC’上的点,且CN=1/4CC’,求证:AB’MN⊥。C'A'CBAB'小结小结2.棱柱的概念4.棱柱的分类3.棱柱的表示5.棱柱的性质6.常见的四棱柱1.多面体的概念