高中数学(直线与椭圆位置关系(二))课件 新人教版选修2-1 课件VIP免费

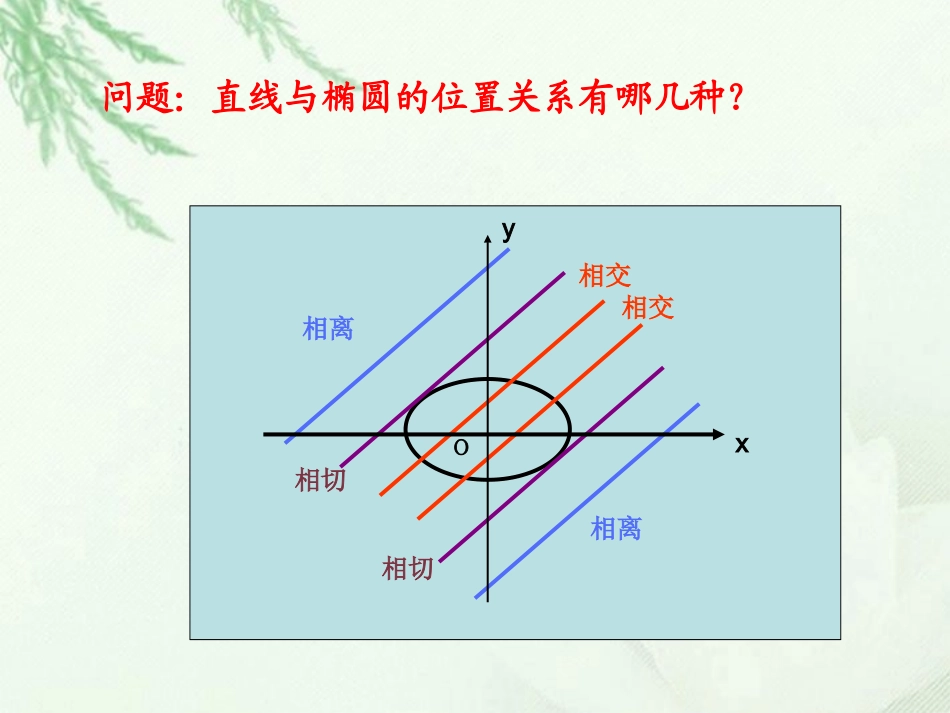
直线与椭圆的位置关系xyO2194xxyx相离相切相交相切相离问题：直线与椭圆的位置关系有哪几种？yＯ相交椭圆与直线的位置关系的判断判断方法这是求解直线与二次曲线有关问题的通法——判别式法判断∆<0，∆=0，∆>0A（x1,y1）直线与椭圆相交的弦长B（x2,y2）思考：当直线与椭圆相交时，如何求被截的弦长？2121224)(1xxxxk221212()()ABxxyy221212()[()()]xxkxbkxb2121kxx12211AByyk借助韦达定理求弦长或过椭圆x216＋y24＝1内一点P(2,1)作一条直线交椭圆于A、B两点，使线段AB被P点平分，求此直线的方程．例例11【思路点拨】由于弦所在直线过定点P(2,1)，所以可设出弦所在直线的方程为y－1＝k(x－2)，(k也可能不存在)与椭圆方程联立，通过中点为P，得出k的值．也可以通过设而不求的思想求直线的斜率．【解】法一：如图，当直线的斜率不存在时，直线的方程是：x-2=0,此时它与椭圆的两交点坐标的中点坐标为（2,0）不符合题意。当直线的斜率存在时，设所求直线的方程为y－1＝k(x－2)，代入椭圆方程并整理，得(4k2＋1)x2－8(2k2－k)x＋4(2k－1)2－16＝0，(*)又设直线与椭圆的交点为A(x1，y1)，B(x2，y2)，则x1、x2是(*)方程的两个根，∴x1＋x2＝82k2－k4k2＋1. P为弦AB的中点，∴2＝x1＋x22＝42k2－k4k2＋1.解得k＝－12，∴所求直线的方程为x＋2y－4＝0.法二：设直线与椭圆交点为A(x1，y1)，B(x2，y2)， P为弦AB的中点，∴x1＋x2＝4，y1＋y2＝2.又 A、B在椭圆上，∴x21＋4y21＝16，x22＋4y22=16.两式相减，得(x21－x22)＋4(y21－y22)＝0，即(x1＋x2)(x1－x2)＋4(y1＋y2)(y1－y2)＝0.∴y1－y2x1－x2＝－x1＋x24y1＋y2＝－12，即kAB＝－12.∴所求直线方程为y－1＝－12(x－2)，即x＋2y－4＝0.中点弦问题求解的关键是充分利用“中点”这一条件，灵活运用中点坐标公式及根与系数的关系．弦中点问题的两种处理方法：（1）法一是设出方程，联立方程组，消去一个未知数，利用韦达定理求出k。（2）“设而不求”，设两端点坐标，代入曲线方程相减可求出弦的斜率。总结总结::变式1：已知椭圆1y2x22斜率(1).求为2的平行弦的中点轨迹方程.(2).过A(2,1)的直线l与椭圆相交,求被截得的弦的中点轨迹方程.（1）由题意可设直线方程为：2yxm联立方程组消去得整理得22222xyyxmy22222()xxm2298220xmxm由韦达定理得1289mxx设交点，中点1122(,),(,)AxyBxy(,)Mxy12121242929()xxmxyymyxxm40xy消参得又由33m4433x434430()xxy所以中点的轨迹方程；M变式2：中心在原点，一个焦点为F1（0,)的椭圆截直线y=3x-2所得弦的中点横坐标为，求椭圆的方程。5021分析：分析：根据题意可设椭圆的标准方程，根据题意可设椭圆的标准方程，与直线方程连里解方程组，利用中点公式求与直线方程连里解方程组，利用中点公式求得弦的中点的横坐标，最后解关于的方得弦的中点的横坐标，最后解关于的方程组即可．程组即可．,abxyo解：设所求椭圆的方程为由得①把直线方程代入椭圆方程，整理得设弦的两个端点为，，则由根与系数的关系得又中点的横坐标为．由此得12222byax)50,0(F5022ba222222(9)12(4)0abxbxba),(11yxA),(22yxB22221912babxx21223ba25,7522ba1257522xy.故所求的椭圆方程为:解①、②得：解①、②得：例2.已知椭圆，直线l：椭圆上是否存在一点，它到直线距离最小？最小距离是多少？192522yx04054yx思考：最大的距离是多少？22221945098225045250xyxycyxcxcxy''解：设与已知直线平行且与椭圆相切的直线L方程为4x-5y+c=0联立方程组25消去整理得L方程为222(8)425(225)3622500025cccc'222240-251515414145LLAB直线与直线的距离为22221,14,,xyyxbbABOAOB已知椭圆方程为直线与椭圆交于，且求椭圆方程。AxyOB),(),,(2211yxByxA解：设02121yyxxOBOA得：则由222441byxxy由2224)1(4bxx0448522...