高中数学 正弦函数的图像课件 北师大版必修4 课件VIP免费

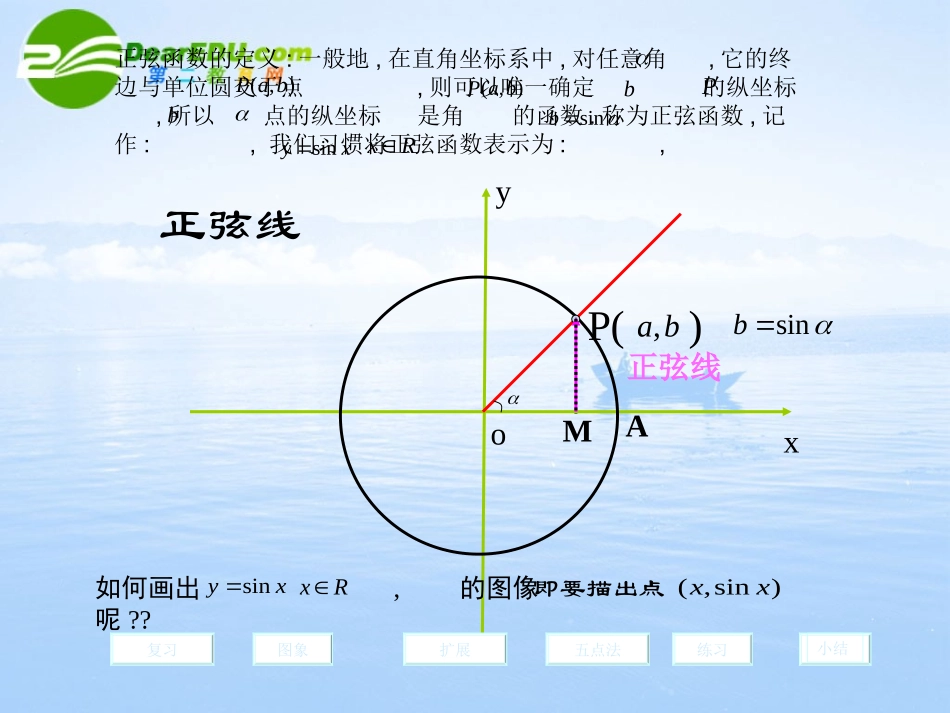
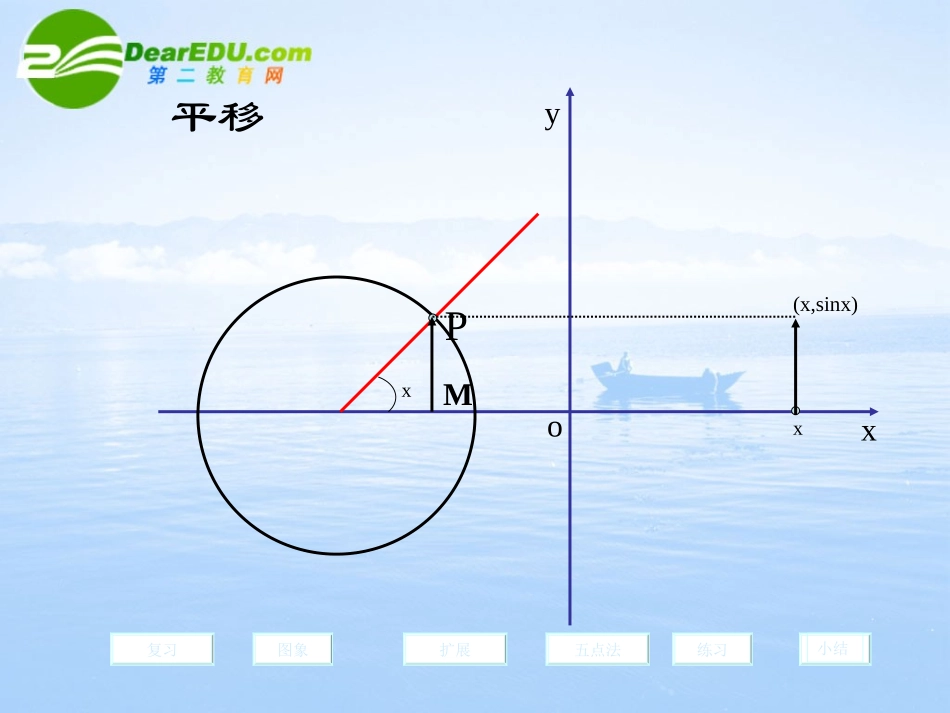
正弦函数的图像第一课时正弦函数的定义:一般地,在直角坐标系中,对任意角,它的终边与单位圆交于点,则可以唯一确定的纵坐标,所以点的纵坐标是角的函数.称为正弦函数,记作:,我们习惯将正弦函数表示为:,xyoP()正弦线MA复习图象五点法扩展练习小结正弦线),(baP),(baPbPbsinbxysinRx如何画出,的图像呢??xysinRxba,sinb即要描出点)sin,(xxxyoPM复习图象五点法扩展练习小结xx(x,sinx)平移.xy63232656734233561120..6323265673423122012222.........1-1.O1y=sinxx[0∈，2π]复习图象五点法扩展练习小结“几何法”作图..y=sinx是个周期函数,周期为2xyy=sin(x)1-102342复习图象五点法扩展练习小结扩展yxy=sinxx[0,2]21-1O(0,0)复习图象五点法扩展练习小结223(,1)2(π，0)23（，-1）（2π，0）“五点法”作图用五点法画正弦函数的图像,五点分别是:(,)(,),(,),(,),(,)0212312000y=2sinx与y=-sinx的图像如何画呢?利用五点法画出y=sinx+1,y=sinx-1及y=2sinx与y=-sinx在(0,)的图像xy=sinxy=sinx+1y=sinx-1π2π关键找”五点”,解:1,列表π23π2012-1-2y=sinx+1y=sinx-12,描点,连线π20001101112200111y=2sinx及y=-sinx的图像xy=sinxy=2sinxy=-sinx2πππ23π2解：１、列表，找五个关键点２、描点，并连线０１２-1-22πππ23π2总结五点法画图的步骤!!!??y=2sinxx)2,0(y=-sinxx)2,0(0000111100000022首先：确立五点的横坐标，分别为：，，，，如何利用五点法画在（0、2）的图像及整个定义域内的图像bxAysin2π23π2其次：求出五点对应的纵坐标。π最后：描点并用光滑的曲线连线0yxoy=1+sinxx[0,2]21-12复习图象五点法扩展练习小结y=sinxx[0,2]比较y=sinx+1的图像可以看成是由y=sinx的图像怎么变换得到啊?小结：首先利用单位圆中的正弦线作出函数y=sinx,x[0,2π]∈的图象，然后以2π为单位，依次向左右平移，得到y=sinxxR∈的图象即正弦曲线，这种作图法叫“几何法”，并通过对图象的分析，得到对正弦函数图象形状起决定作用的五个点，并总结出“五点法”这种简洁的作图法。复习图象五点法扩展练习小结作业:•课本页第一小题•回去观察正弦函数的图像归纳其性质,并完成后面的作业•多谢各位老师前来指点!20P