高中数学 第二章指数函数(1)课件 苏教版必修1 课件VIP免费

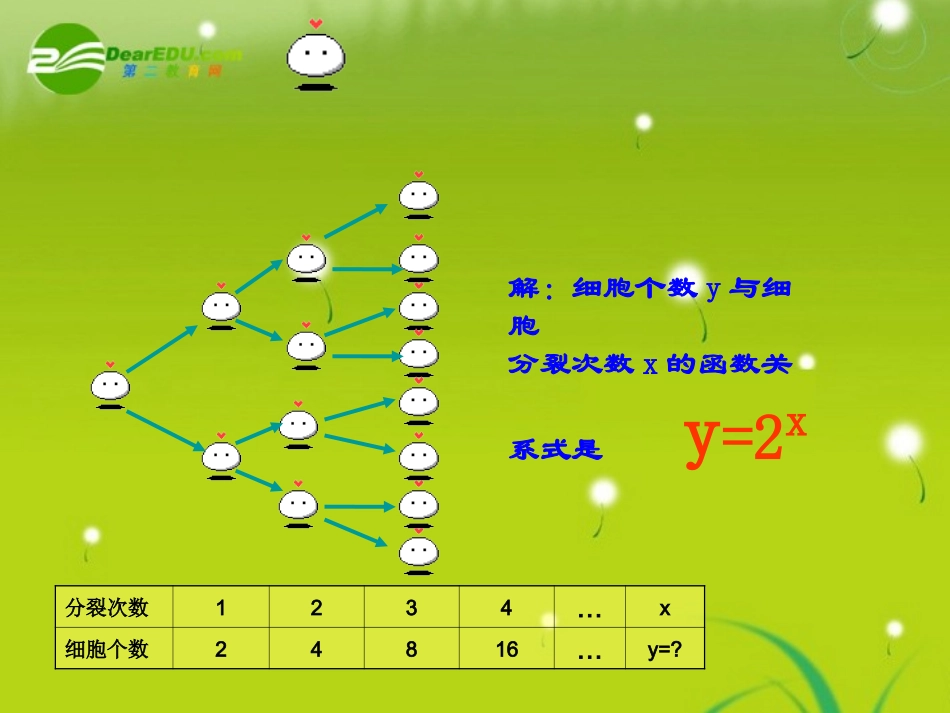
少小不学习，老来徒伤悲成功=艰苦的劳动+正确的方法+少谈空话天才就是百分之一的灵感，百分之九十九的汗水！天才在于勤奋，努力才能成功！2025年2月24日知识改变命运,勤奋创造奇迹.•有一种细胞分裂时，由1个分裂成2个，2个分裂成4个，3个分裂成8个,···,1个这样的细胞分裂x次后得到y个细胞。？：你能总结出细胞个数y与细胞分裂次数x的关系式吗？情景1情景1分裂次数1234…x细胞个数24816…y=?解：细胞个数y与细胞分裂次数x的函数关系式是y=2x情景2:庄子曰：一尺之棰，日取其半，万世不竭。庄子曰：一尺之棰，日取其半，万世不竭。解：木棒长度y与经历天数x的关系式是)21(xy设问1：212,()21,,xxyxyxyx象y这类函数与我们刚学过的y一样吗？这两类函数有什么区别?你能从以上两个解析式中抽象出一个更具有一般性的函数模型吗？结论：y=ax，这是一类重要的函数模型，并且有广泛的用途，它可以解决好多生活中的实际问题，这就是我们下面所要研究的一类重要函数模型。一、指数函数的概念：一般地，函数y=ax(a>0，a≠1)叫做指数函数，其中x是自变量，函数的定义域是R。为什么要规定a>0，a≠1?当a=0时，若x>0则若x≤0则当a<0时，当a=1时，为了便于研究，规定：a>0且a≠10xaxa无意义122xa不一定有意义，如（）11xy时常量y=ax中a的范围：例1、判断下列函数是否是指数函数23xy13xy3xyxy3)121()12(aaayx，且xy)4(xy24xyxxy思考题:已知函数y=是指数函数，那么a的取值范围你能算出吗？xaaa2322设问2：我们研究函数的性质，通常都研究哪几个性质？通过什么方法去研究？设问3：得到函数的图象一般用什么方法？列表、求对应的x和y值、描点作图列表、求对应的x和y值、描点作图用描点法绘制的草图：2xy用描点法绘制的草图：(0.5)xy定义域、值域、单调性、奇偶性图象12()()2xxyxRyx比较函数与函数的图像,得出指数函数y=a的性质R）x（）21（yxy=1R）x（2yx-1-4-3-2-1011223434xy(0,1)两函数图象有什么共同点，又有什么不同特征?影响函数图象特征的主要因素是什么？Oxy(0,1)y=1xayOxy(0,1)y=1xay定义域：值域：奇偶性：在R上是增函数在R上是减函数单调性：R),0(非奇非偶函数定点：过点（0，1）x>0时，y>1;x<0时,00时，011a10a图象性质定义域：R值域：),0(奇偶性：非奇非偶函数定点：过点(0，1)单调性：例2:比较下列各组数的大小：（1）1.7和1.7(2)0.8和0.8(3)3.25和2.53-0.1-0.2-4.3Oxy(0，1)y=0.8x-0.1-0.2yx(0，1)y=1.7x2.53分析:(1)1.7和1.7可以看作函数y=1.7当x分别为2.5和3时的函数值2.53x指数函数图象与性质的应用：1.11.1(4)1.31.2和2.22.3比较大小的方法：(1)构造函数法：数的特征是同底不同指(包括可转化为同底的数);利用指数函数的单调性比较.(2)搭桥比较法:用特殊的值0或1来连接两数进行比较.(3)作差(商)比较法指数函数图象与性质的应用：例3、指数函数的图象如下图所示，则底数,,,abcd与正整数11共五个数，从小到大的顺序是：.xy01xyaxybxydxyc01badca,b,c,dxydxycxyaxyb,,,xxxxyaybycyd(1)底数大于1时,底数越大图象越靠近y轴；(2)底数小于１时,底数越小越靠近y轴．1C2C3C4C1YXO21,31,3,2)(3,2,21,31)(31,21,2,3)(31,3,21,2)(DCBAaxay31,3,21,2练习：如图，曲线是指数函的图象，已知取四个值，则相应于曲线的依次为（）1234CCCC、、、aD课堂练习:π(1)与8.0418.121(2)与125877378(4)与3.008.11.398.0(3)与123->><>1、比较大小3、已知y=f（x）是指数函数，且f(2)=4，求函数y=f（x）的解析式。2、已知，比较a.b的大小。44()()77ab４、若是一个指数函数，求的取值范围。(31)xyaa５、如果对于一切成立，则正数的大小关系为：xxmn0x,mn点滴收获：1.本节课学习了那些知识?指数函数的定义2.如何记忆指数函数的性质?指数函数的图象及性质(1)xyaa(01)xyaa记住两个基本图形1xoyy=1指数函数图象的简单应用再见