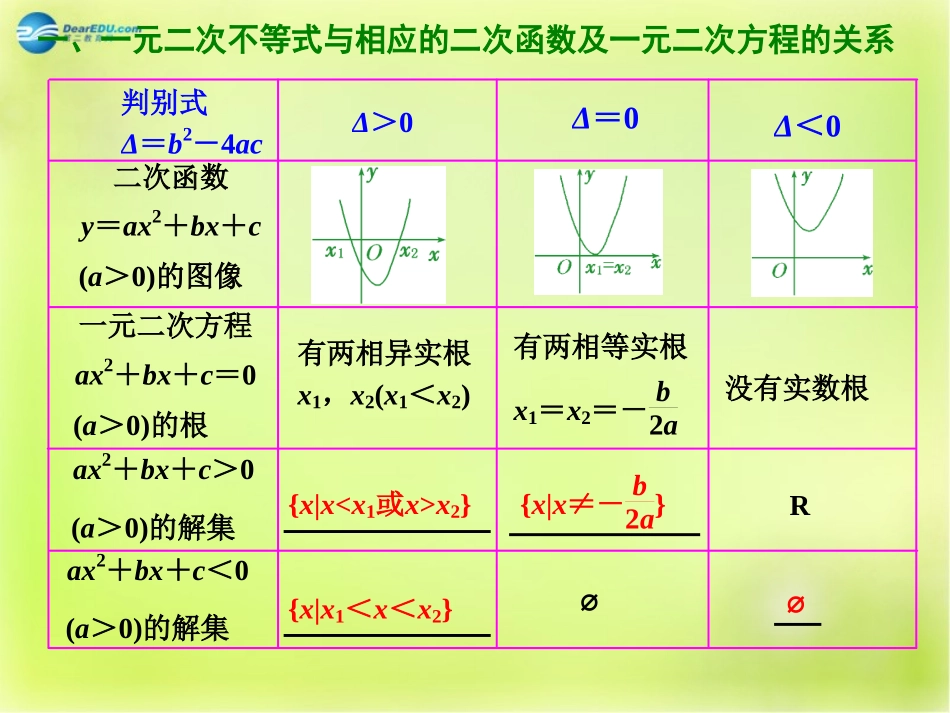
第二节一元二次不等式及其解法判别式Δ=b2-4acΔ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0)的图像一元二次方程ax2+bx+c=0(a>0)的根ax2+bx+c>0(a>0)的解集ax2+bx+c<0(a>0)的解集有两相异实根x1,x2(x1<x2)有两相等实根x1=x2=-b2a没有实数根{x|xx2}{x|x≠-b2a}R{x|x1<x<x2}∅∅一、一元二次不等式与相应的二次函数及一元二次方程的关系1、解下列不等式:0<x2-x-2≤4转化为二元一次不等式组求解.2.不等式ax2+bx+2>0的解集是-12,13,则a+b的值是()A.10B.-10C.14D.-14解析:由题意知-12、13是ax2+bx+2=0的两根.则a=-12,b=-2.a+b=-14.故选.D3.不等式x2+ax+4<0的解集不是空集,则实数a的取______.解析: 不等式x2+ax+4<0的解集不是空集,∴Δ=a2-4×4>0,即a2>16.∴a>4或a<-4.答案:(-∞,-4)∪(4,+∞)[典例]解下列不等式:x2-4ax-5a2>0(a≠0).分类讨论(含参数的一元二次不等式的解法)[类题通法]1.解一元二次不等式的一般步骤:(1)对不等式变形,使一端为0且二次项系数大于0,即ax2+bx+c>0(a>0),ax2+bx+c<0(a>0);(2)计算相应的判别式;(3)当Δ≥0时,求出相应的一元二次方程的根;(4)根据对应二次函数的图像,写出不等式的解集.2.解含参数的一元二次不等式,要把握好分类讨论的层次,一般按下面次序进行讨论:首先根据二次项系数的符号进行分类,其次根据根是否存在,即Δ的符号进行分类,最后在根存在时,根据根的大小进行分类.解下列不等式:[针对训练]ax2-(a+1)x+1<0(a>0).【知识梳理二】由二次函数图像与一元二次不等式的关系得到的两个常用结论(1)不等式ax2+bx+c>0对任意实数x恒成立⇔a=b=0,c>0,或a>0,Δ<0.(2)不等式ax2+bx+c<0对任意实数x恒成立⇔a=b=0,c<0,或a<0,Δ<0.1、若不等式mx2+2mx+1>0的解集为R,则m的取值范围______.答案:[0,1)解析:①当m=0时,1>0显然成立.②当m≠0时,由条件知m>0,Δ=4m2-4m<0.得06时,f(x)的值恒大于零等价于f(-1)=1+(a-4)×(-1)+4-2a>0,解得a<3,故有a∈∅;②当-1≤4-a2≤1,即2≤a≤6时,角度二形如f(x)≥0(x∈[a,b])确定参数范围2.对任意x∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,求a的取值范围.只要f4-a2=4-a22+(a-4)×4-a2+4-2a>0,即a2<0,故有a∈∅;③当4-a2>1,即a<2时,只要f(1)=1+(a-4)+4-2a>0,即a<1,故有a<1.综上可知,当a<1时,对任意x∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零.解:由f(x)=x2+(a-4)x+4-2a=(x-2)a+x2-4x+4,令g(a)=(x-2)a+x2-4x+4.由题意知在[-1,1]上,g(a)的值恒大于零,∴g-1=x-2×-1+x2-4x+4>0,g1=x-2+x2-4x+4>0,解得x<1或x>3.故当x<1或x>3时,对任意的a∈[-1,1],函数f(x)的值恒大于零.角度三形如f(x)≥0(参数m∈[a,b])确定x的范围3.对任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,求x的取值范围.[类题通法]恒成立问题及二次不等式恒成立的条件(1)解决恒成立问题一定要清楚选谁为主元,谁是参数.一般地,知道谁的范围,就选谁当主元,求谁的范围,谁就是参数.(2)对于二次不等式恒成立问题,恒大于0就是相应的二次函数的图像在给定的区间上全部在x轴上方;恒小于0就是相应的二次函数的图像在给定的区间上全部在x轴下方.[典例]某小商品2013年的价格为8...