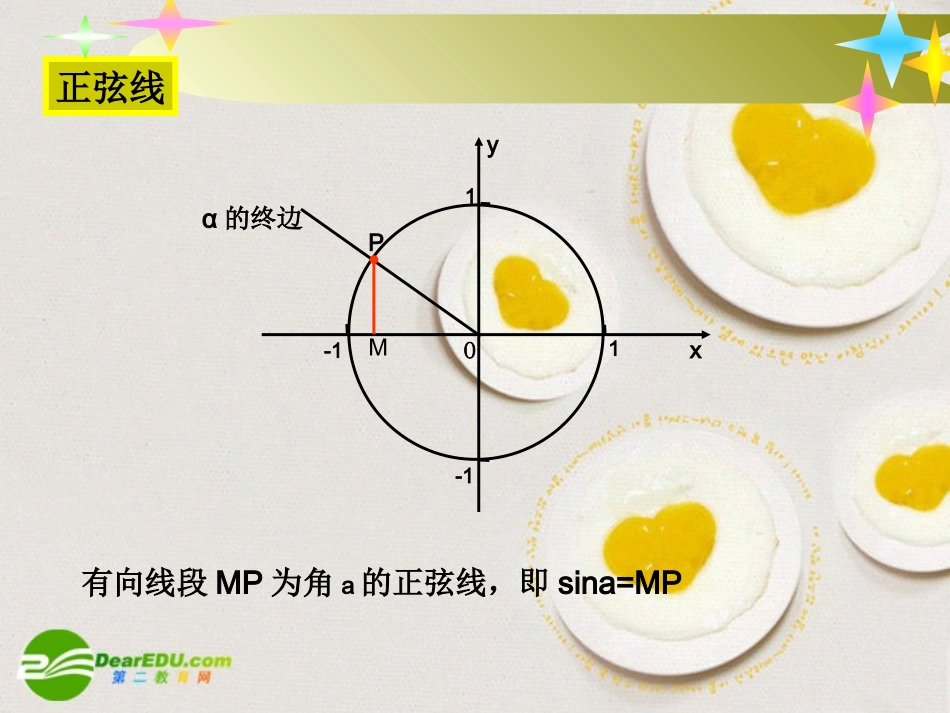
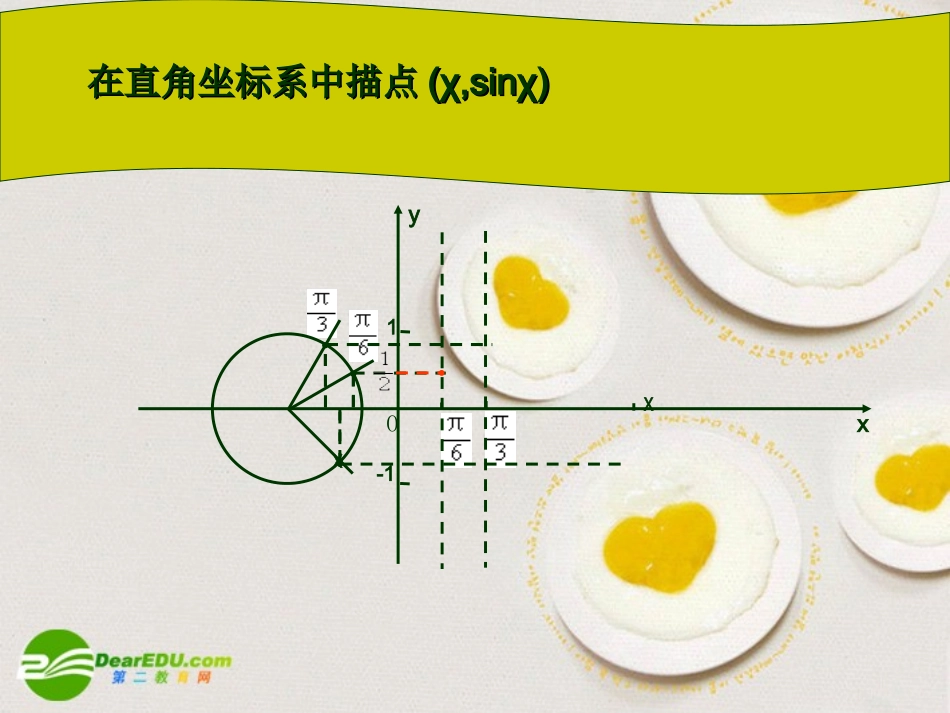
xyOα的终边PM正弦线有向线段MP为角a的正弦线,即sina=MP1-11-1Oxy在直角坐标系中描点在直角坐标系中描点(χ,sinχ)(χ,sinχ)-11χχ用几何法作y=sinx,x∈[0,2π]上的图象•作直角坐标系,并在y轴左侧任取一点O1作单位圆•将单位圆和x轴上0~2π这一段12等分•作出正弦线,并平移到相应的位置上•用光滑曲线把正弦线的终点联结起来,就得到了函数y=sinx,x[0,2∈π]的图象yOxπ2π01-11y=sinx,x∈[0,2π]y=sinx,x∈[0,2π]yx-11y=sinx,x∈R-4π-2πy=sinx,xR∈的图象•将y=sinx,x[0,2∈π]的图象左、右平移(每次2π个单位长度)就可以得到正弦函数y=sinx,xR∈的图象•正弦函数y=sinx,xR∈的图象叫做正弦曲线-3π-ππ2π3π4π0例1:下列命题正确的个数是()(1)y=sinx,xR∈与y=sinx,x[0∈,2π]是相同函数(2)函数y=sinx,x[2π∈,4π]可由y=sinx,x[0∈,2π]向左平移2π个单位长度而得到。(3)作正弦函数图象时,单位圆的半径长与y轴上的单位一致,与x轴上的单位可以不一致。(4)正弦函数不超过两直线y=1和y=-1所夹范围。A、1个B、2个C、3个D、4个Aπy=sinx,x∈[0,2π]Oy2π作y=sinx,x[0,2∈π]的简图(0,0)(π,0)(2π,0)(,1)(,-1)x““五点法”五点法”1-1例2画出函数y=1+sinx,x[0,2π]∈的简图解:按五个关键点列表:11+sinx0sinx102ππ100xyx21-10y=1+sinx,x[0,2π]∈y=sinx,x[0,2π]∈210-1π2π描点画图:•掌握函数y=sinx,x∈[0,2π]与函数y=sinx,x∈R之间的关系•掌握正弦曲线的图象形状。•用五点法画正弦曲线和与正弦曲线有关的某些简单函数,在长度为2π的闭区间上的简图。思考题:作出y=|sinx|,x[π∈,3π]的图象