高中数学平面向量基本定理课件人教版必修4B 课件VIP免费

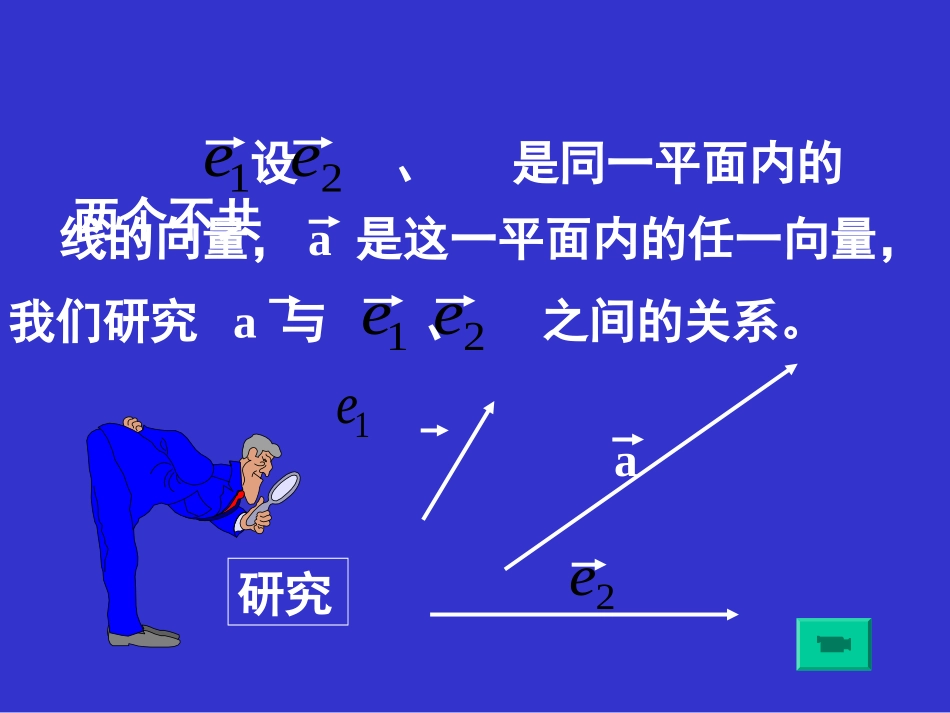
平平平平平平平平2.3.1平面向量的基本定理设、是同一平面内的两个不共1e2e线的向量，a是这一平面内的任一向量，1e2e我们研究a与、之间的关系。1ea2e研究OC=OM+ON=21OA+OB11e2e2即a=+.1ea1eA2eOaCB2eNMMN平面向量基本定理一向量a有且只有一对实数、使21共线向量，那么对于这一平面内的任如果、是同一平面内的两个不1e2e11ea=+2e2示这一平面内所有向量的一组基底。我们把不共线的向量、叫做表1e2e（1）一组平面向量的基底有多少对？（有无数对）思考EFANBaMOCNMMOCNaE思考(2)若基底选取不同，则表示同一向量的实数、是否相同？21（可以不同，也可以相同）OCFMNaEEABNOC=2OB+ONOC=2OA+OEOC=OF+OE特别的，若a=0，则有且只有：可使0=11e2e2+.21==0？若与中只有一个为零，情况会是怎样？21特别的，若a与（）共线，则有=0（=0），使得:a=+.121e22e2e11e已知向量求做向量-2.5+3例3：、1e2e1e2e1e2e15.2e23eOABC·1eOABC·?MMDMCMBMAbabADaABABCD、、、表示、，用，且，的两条对角线相交于点如图所示，平行四边形例4DCBAM例５ABCD中，E、F分别是DC和AB的中点，试判断AE,CF是否平行？FBADCEFBADCEE、F分别是DC和AB的中点,AE=AD+DE=b+a2121CF=CB+BF=-b-aAE=-CFAE与CF共线，又无公共点AE,CF平行.解：设AB=a,AD=b.总结：1、平面向量基本定理内容2、对基本定理的理解（1）实数对λ1、λ２的存在性和唯一性（２）基底的不唯一性（３）定理的拓展性３、平面向量基本定理的应用求作向量、解（证）向量问题、解（证）平面几何问题例5、如图，已知梯形ABCD，AB//CD，且AB=2DC,M,N分别是DC,AB的中点.请大家动手,在图中确定一组基底，将其他向量用这组基底表示出来。ANMCDB解析：BC=BD+DC=MN=DN-DM21=(AN-AD)-DC(AD–AB)+DCANMCDBDC=AB=21211e设AB=,AD=,则有：1e2e41=-.2e1e1e2e1e21=-+=2141=--2e1e1e2e211e-+评析能够在具体问题中适当地选取基底，使其他向量能够用基底来表示，再利用有关知识解决问题。设a、b是两个不共线的向量，已知AB=2a+kb,CB=a+3b,CD=2a–b,若A、B、D三点共线，求k的值。A、B、D三点共线解：AB与BD共线，则存在实数λ使得AB=λBD.λ使得AB=λBD.思考k=8.=a–4b由于BD=CD–CB=(2a–b)–(a+3b)则需2a+kb=(a–4b)由向量相等的条件得2=k=4则需2a+kb=(a–4b)2-=0k–4=0此处可另解：k=8.即（2-）a+(k-4)b=0本题在解决过程中用到了两向量共线的充要条件这一定理，并借助平面向量的基本定理减少变量，除此之外，还用待定系数法列方程，通过消元解方程组。这些知识和考虑问题的方法都必须切实掌握好。评析2.在实际问题中的指导意义在于找到表示一个平面所有向量的一组基底（不共线向量与），从而将问题转化为关于、的相应运算。1e2e1e2e1.平面向量基本定理可以联系物理学中的力的分解模型来理解，它说明在同一平面内任一向量都可以表示为不共线向量的线性组合，该定理是平面向量坐标表示的基础，其本质是一个向量在其他两个向量上的分解。课堂总结思考在梯形ABCD中，E、F分别时AB、CD的中点，用向量的方法证明：EF//AD//BC,且EF=(AD+BC)21谢谢同学们谢谢同学们再见