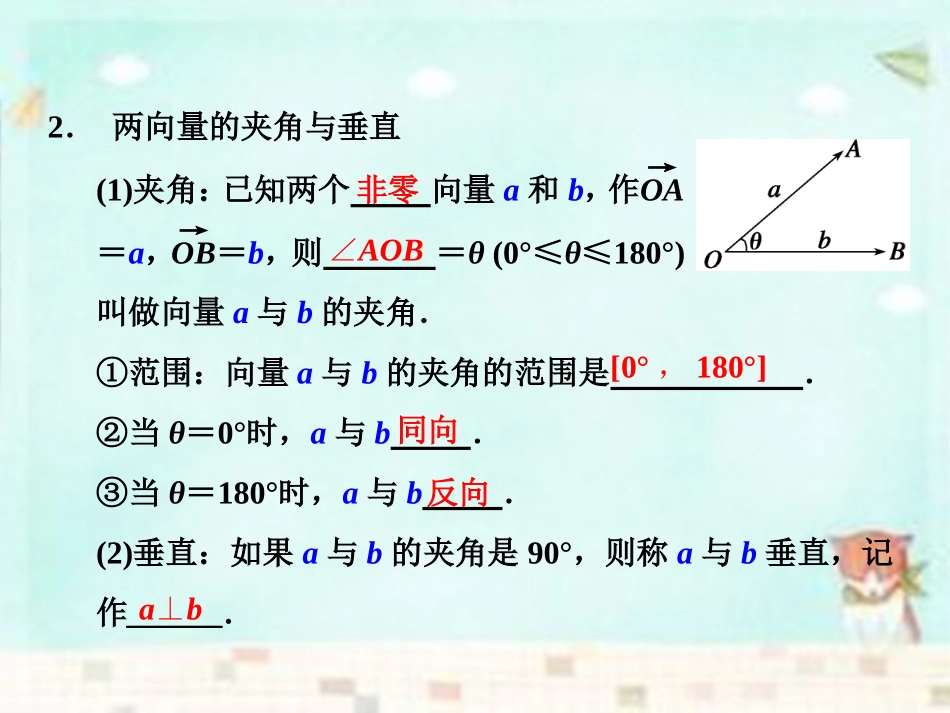
1.平面向量基本定理(1)定理:如果e1,e2是同一平面内的两个向量,那么对于这一平面内的向量a,实数λ1,λ2,使a=λ1e1+λ2e2.(2)基底:把的向量e1,e2叫做表示这一平面内向量的一组基底.不共线任意有且只有一对不共线所有2.两向量的夹角与垂直(1)夹角:已知两个向量a和b,作OA→=a,OB→=b,则=θ(0°≤θ≤180°)叫做向量a与b的夹角.①范围:向量a与b的夹角的范围是.②当θ=0°时,a与b.③当θ=180°时,a与b.(2)垂直:如果a与b的夹角是90°,则称a与b垂直,记作______.非零∠AOB[0°,180°]同向反向a⊥b探究点一平面向量基本定理的提出(1)平面内的任何向量都能用这个平面内两个不共线的向量来表示.如图所示,e1,e2是两个不共线的向量,试用e1,e2表示向量AB→,CD→,EF→,GH→,HG→,a.通过观察,可得:AB→=_________,CD→=_________,EF→=_________,GH→=_____________,HG→=___________,a=______.2e1+3e2-e1+4e24e1-4e2-2e1+5e22e1-5e2-2e1(2)平面向量基本定理的内容是什么?什么叫基底?答平面向量基本定理是指:如果e1、e2是同一平面内的两个不共线向量,那么对于这一平面内的任意向量a,有且只有一对实数λ1、λ2,使a=λ1e1+λ2e2.这里不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底.探究点二平面向量基本定理的证明(1)证明定理中λ1,λ2的存在性.如图,e1,e2是平面内两个不共线的向量,a是这一平面内任一向量,a能否表示成λ1e1+λ2e2的形式,请通过作图探究a与e1、e2之间的关系.答在平面内任取一点O,作OA→=e1,OB→=e2,OC→=a,过点C分别作平行于OB,OA的直线,交直线OA于点M,交直线OB于点N,有OM→=λ1OA→,ON→=λ2OB→, OC→=OM→+ON→,∴a=λ1e1+λ2e2,如图所示.(2)证明定理中λ1,λ2的唯一性.如果e1、e2是同一平面内的两个不共线的向量,a是和e1、e2共面的任一向量,且存在实数λ1、λ2使a=λ1e1+λ2e2,证明λ1,λ2是唯一确定的.(提示:利用反证法)答假设存在另一组实数λ′1,λ′2也能使a=λ′1e1+λ′2e2成立,则λ′1e1+λ′2e2=λ1e1+λ2e2.∴(λ′1-λ1)e1+(λ′2-λ2)e2=0. e1、e2不共线,∴λ′1-λ1=λ′2-λ2=0,∴λ′1=λ1,λ′2=λ2.∴使a=λ1e1+λ2e2成立的实数对λ1,λ2是唯一的.探究点三向量的夹角(1)已知a、b是两个非零向量,过点O作出它们的夹角θ.答过点O作OA→=a,OB→=b,则∠AOB=θ,就是a与b的夹角.(2)两个非零向量夹角的范围是怎样规定的?确定两个向量夹角时,要注意什么事项?答两个非零向量夹角的范围是0°≤θ≤180°,确定两个向量夹角时要注意先使向量的始点相同,再确定大小.(3)在等边三角形ABC中,试写出下面向量的夹角:a.〈AB→,AC→〉=;b.〈AB→,CA→〉=;c.〈BA→,CA→〉=;d.〈AB→,BA→〉=.60°120°60°180°【典型例题】例1已知e1,e2是平面内两个不共线的向量,a=3e1-2e2,b=-2e1+e2,c=7e1-4e2,试用向量a和b表示c.解 a,b不共线,∴可设c=xa+yb,则xa+yb=x(3e1-2e2)+y(-2e1+e2)=(3x-2y)e1+(-2x+y)e2=7e1-4e2.又 e1,e2不共线,∴3x-2y=7,-2x+y=-4.解得x=1,y=-2,∴c=a-2b.小结选定基底之后,就要“咬定”基底不放,并围绕它做中心工作,千方百计用基底表示目标向量.这有时要利用平面几何知识.要注意将平面几何知识中的性质、结论与向量知识有机结合,具体问题具体分析解决.跟踪训练1如图所示,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知AM→=c,AN→=d,试用c,d表示AB→,AD→.解设AB→=a,AD→=b,则AM→=AD→+DM→=AD→+12AB→=12a+b,①AN→=AB→+BN→=AB→+12AD→=a+12b②由①②得12a+b=ca+12b=d,解得a=-23c+43db=43c-23d,即AB→=-23c+43d,AD→=43c-23d.例2如图,梯形ABCD中,AB∥CD,且AB=2CD,M、N分别是DC和AB的中点,若AB→=a,AD→=b,试用a、b表示DC→、BC→、MN→.解如图所示,连接CN,则四边形ANCD是平行四边形.则DC→=AN→=12AB→=12a,BC→=N...