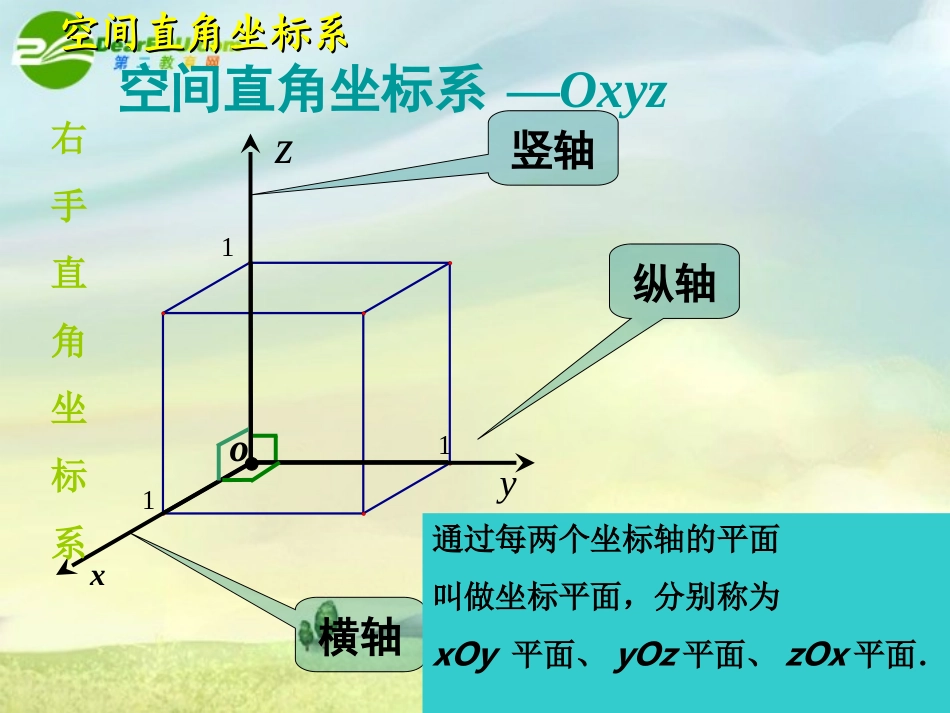
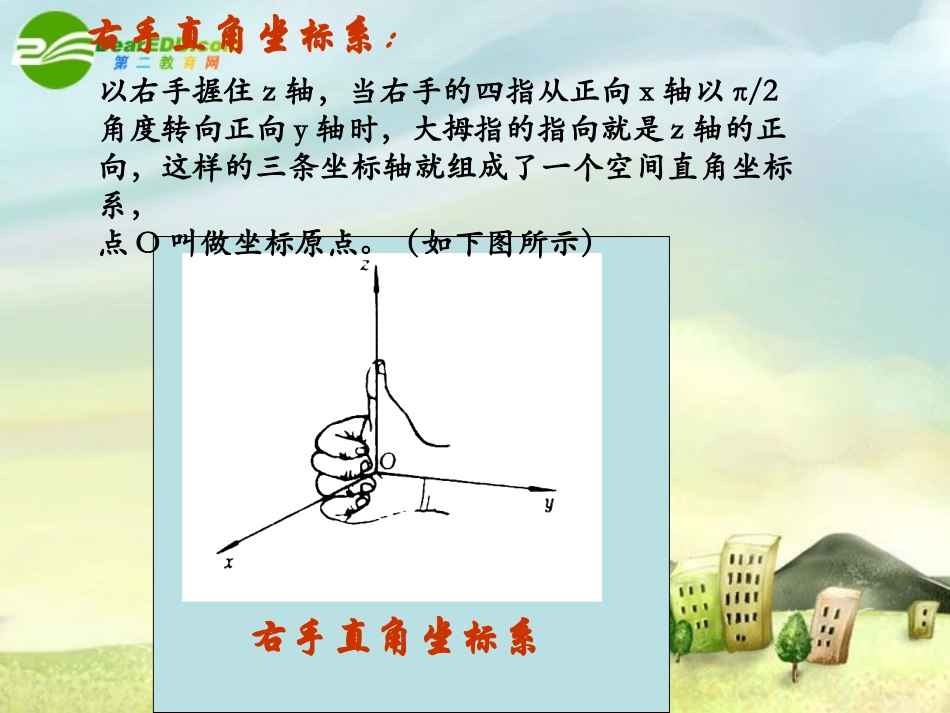
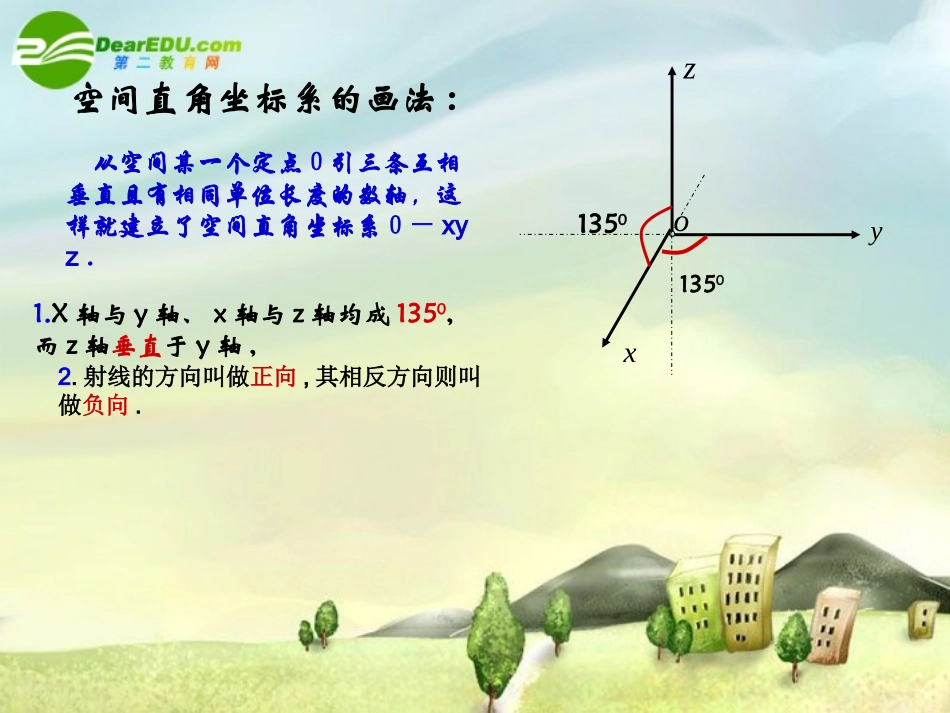
xo右手直角坐标系空间直角坐标系yz—Oxyz横轴纵轴竖轴111空间直角坐标系空间直角坐标系通过每两个坐标轴的平面叫做坐标平面,分别称为xOy平面、yOz平面、zOx平面.右手直角坐标系:右手直角坐标系以右手握住z轴,当右手的四指从正向x轴以π/2角度转向正向y轴时,大拇指的指向就是z轴的正向,这样的三条坐标轴就组成了一个空间直角坐标系,点O叫做坐标原点。(如下图所示)从空间某一个定点0引三条互相垂直且有相同单位长度的数轴,这样就建立了空间直角坐标系0-xyz.xyzo13501350空间直角坐标系的画法:1.X轴与y轴、x轴与z轴均成1350,而z轴垂直于y轴,2.射线的方向叫做正向,其相反方向则叫做负向.设点M是空间的一个定点,过点M分别作垂直于x轴、y轴和z轴的平面,依次交x轴、y轴和z轴于点P、Q和R.空间直角坐标系空间直角坐标系yxzM’O设点P、Q和R在x轴、y轴和z轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).MRQP反过来,给定有序实数组(x,y,z),我们可以在x轴、y轴和z轴上依次取坐标为x,y和z的点P、Q和R,分别过P、Q和R各作一个平面,分别垂直于x轴、y轴和z轴,这三个平面的唯一交点就是有序实数组(x,y,z)确定的点M.空间直角坐标系空间直角坐标系yxzM’OMRQP空间直角坐标系空间直角坐标系yxzPM’QOMR这样空间一点M的坐标可以用有序实数组(x,y,z)来表示,有序实数组(x,y,z)叫做点M在此空间直角坐标系中的坐标,记作M(x,y,z).其中x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标.空间的点有序数组),,(zyx11Mxyzo(,,)xyz空间中点的坐标PQR空间直角坐标系空间直角坐标系Mxyzo(,,)xyz空间中点的坐标(方法二)(0,0,0)PQRA(,0,0)x(0,,0)y(0,0,)z(,,0)xy空间直角坐标系空间直角坐标系C'D'B'A'COAByzxxOy平面是坐标形如的点构成的x轴上的点纵坐标竖坐标为.z轴上的点横坐标纵坐标为.y轴上的点横坐标竖坐标为.二、坐标平面内的点一、坐标轴上的点yOz平面是坐标形如的点构成的xOz平面是坐标形如的点构成的探究问题探究问题000(x,y,0)(0,y,z)(x,0,z)yxzABC'A'B'C'DOOABC—D’A’B’C’是单位正方体.以O为原点,分别以射线OA,OC,OD’的方向为正方向,以线段OA,OC,OD’的长为单位长,建立空间直角坐标系O—xyz.试说出正方体的各个顶点的坐标.并指出哪些点在坐标轴上,哪些点在坐标平面上.空间直角坐标系空间直角坐标系(0,0,0)(1,0,0)(1,1,0)(0,1,0)(1,0,1)(1,1,1)(0,1,1)(0,0,1)练一练.P例1如下图,在长方体中,,写出四点D’,C,A’,B’的坐标.''''CBADOABC3||OA4||OC2||'OD'D2'OD'D解:在z轴上,且,它的竖坐标是2;它的横坐标x与纵坐标y都是零,所以点的坐标是(0,0,2).点C在y轴上,且,它的纵坐标是4;它的横坐标x与竖坐标z都是零,所以点C的坐标是(0,4,0).同理,点的坐标是(3,0,2).4'OC'AOyxzACB'B'A'C'D典型例题典型例题例1如下图,在长方体中,,写出四点D’,C,A’,B’的坐标.''''CBADOABC3||OA4||OC2||'ODOyxzACB'B'A'C'D典型例题典型例题解:点B’在平面上的射影是B,因此它的横坐标x与纵坐标y同点B的横坐标x与纵坐标y相同.在xOy平面上,点B横坐标x=3,纵坐标y=4;点B’在z轴上的射影是D’,它的竖坐标与点D’的竖坐标相同,点D’的竖坐标z=2.所以点B’的坐标是(3,4,2).Ⅶxyoz坐标面把空间分成八个部分ⅠⅡⅢⅣⅤⅥⅧ每一个部分叫卦限通过每两个坐标轴的平面叫坐标平面在空间直角坐标系中,作出点A(1,4,4).例解:oxyzO从原点出发沿x轴正方向移动1个单位P1P1沿与y轴平行的方向向右移动4个单位P2P2沿与z轴平行的方向向上移动4个单位AA(1,4,4)P244那么点B(1,4,-4)又怎样画呢?P11点M(x,y,z)是空间直角坐标系Oxyz中的一点,写出满足下列条件的点的坐标(1)与点M关于x轴对称的点(2)与点M关于y轴对称的点(3)与点M关于z轴对称的点(4)与点M关于原点对称的点(5)与点M关于xOy平面对称的点(6)与点M关于xOz平面对称的点(7)与点M关于yOz平面对称的点(x,-y,-z)(-x,y,-z)(-x,-y,z)(-x,-y,-z)(x,y,-z)(x,-y,z)(-x,y,z)探究问题探究问题总结:关于谁谁不变,其余的相反