高中数学 第二章 基本初等函数Ⅰ章末专题整合课件 新人教A版必修1 课件VIP免费

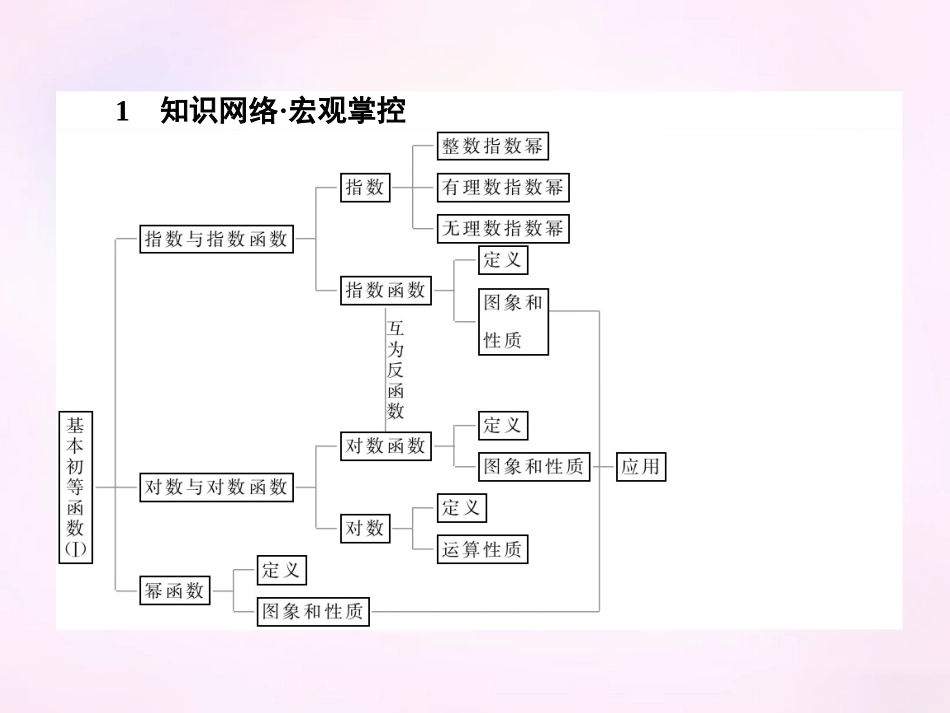
第二章章末专题整合1知识网络·宏观掌控2热点透视·专题突破热点一指数与对数的运算例12015·山东德州市高一期中求值：(1)21412－(－9.6)0－33823＋(1.5)－2；(2)log2512·log45－log133－log24＋55log2.解析：(1)原式＝9412－1－27823＋32－2＝32－1－32－2＋232＝32－1－49＋49＝12.(2)原式＝－12log52·12log25＋log33－2log22＋2＝－14＋1－2＋2＝34.热点二指数函数的图象与性质例22015·山东德州市高一期中已知奇函数f(x)＝12x－1＋a.(1)求f(x)的定义域；(2)求a的值；(3)证明x＞0时，f(x)＞0.解析：(1) 2x－1≠0，即2x≠1，∴x≠0，故f(x)的定义域是(－∞，0)∪(0，＋∞)．(2) f(x)是奇函数，又 f(－x)＝12－x－1＋a＝2x1－2x＋a，∴f(x)＋f(－x)＝12x－1＋a＋2x1－2x＋a＝0.∴a＝12.(3)证明：当x＞0时，2x＞1，∴2x－1＞0.∴12x－1＋12＞0，即x＞0时，f(x)＞0.热点三对数函数的图象与性质例32015·江西临川一中高一期末已知函数f(x)＝lg(x＋1)，g(x)＝2lg(2x＋t)(t为参数)．(1)写出函数f(x)的定义域和值域；(2)当x∈[0,1]时，如果f(x)≤g(x)，求参数t的取值范围．解析：(1)定义域为(－1，＋∞)，值域为R.(2)由f(x)≤g(x)，得lg(x＋1)≤2lg(2x＋t)，得x＋1≤(2x＋t)2在x∈[0,1]恒成立，得t≥x＋1－2x在x∈[0,1]恒成立．令u＝x＋1(u∈[1，2])，解得x＝u2－1，得h(x)＝x＋1－2x＝－2u2＋u＋2(u∈[1，2])最大值为1，故t的取值范围是[1，＋∞).热点四幂函数的图象与性质例42015·安徽亳州一中高一月考已知幂函数y＝f(x)经过点2，18.(1)试求函数解析式；(2)判断函数的奇偶性并写出函数的单调区间．解析：(1)由题意，得f(2)＝2a＝18，a＝－3，故函数解析式为f(x)＝x－3.(2)定义域为(－∞，0)∪(0，＋∞)，关于原点对称，因为f(－x)＝(－x)－3＝－x－3＝－f(x)，所以该幂函数为奇函数，其单调减区间为(－∞，0)，(0，＋∞)．【专题突破】1.2015·山东德州市高一期中若f(x)，g(x)分别为R上的奇函数，偶函数，且满足f(x)－g(x)＝ex，则有()A．f(2)＜f(3)＜g(0)B．g(0)＜f(3)＜f(2)C．f(2)＜g(0)＜f(3)D．g(0)＜f(2)＜f(3)解析：用－x代换x得：f(－x)－g(－x)＝－f(x)－g(x)＝e－x，联立fx－gx＝ex，－fx－gx＝e－x解得f(x)＝ex－e－x2，g(x)＝－ex＋e－x2.显然f(x)在其定义域内是增函数，而f(0)＝0，g(0)＝－1，所以g(0)＜f(2)＜f(3)，故选D.答案：D2．(2015·山东临沂市高一期末)函数f(x)＝14x＋12x－1，x∈[0，＋∞)的值域为()A.－54，1B.－54，1C．(－1,1]D．[－1,1]解析：令t＝12x，则t∈(0,1]，函数f(x)化为y＝t2＋t－1＝t＋122－54，该函数在则(0,1]上单调递增，当t＝0时，y＝－1；当t＝1时，y＝1，所以其值域为(－1,1]，故选C.答案：C3.2015·河北邯郸市高一期末已知f(3x)＝2xlog2x，那么f(3)的值是()A．8log23B．2C．0D．－2解析：令x＝1，得f(3)＝2log21＝0，故选C.答案：C4.2015·宁夏大学附中高一期中已知函数f(x)在[0，＋∞)上是增函数，g(x)＝－f(|x|)，若g(lgx)＞g(l)，则x的取值范围是()A.110，10B．(0,10)C．(10，＋∞)D.110，10∪(10，＋∞)解析：因为g(lgx)＞g(l)，所以f(|lgx|)＜f(1)，又f(x)在[0，＋∞)单调递增，所以0≤|lgx|＜1，解得110＜x＜10，故选A.答案：A5.2015·河北沧州市高一期末已有幂函数f(x)＝(m－3)xm，则下列关于f(x)的说法不正确的是()A．f(x)的图象过原点B．f(x)的图象关于原点对称C．f(x)的图象关于y轴对称D．f(x)＝x4解析：由题意得m－3＝1，m＝4，f(x)＝x4，其图象关于y轴对称，且过原点，故选B.答案：B6.2015·河南许昌高一四校联考已知函数f(x)＝x223mm－＋＋(m∈Z)为偶函数，且f(3)＜f(5)．(1)求m的值，并确定f(x)的解析式；(2)若y＝loga[f(x)－ax](a＞0，且a≠1)在区间[2,3]上为增函数，求实数a的取值范围．解析：(1) f(x)是偶函数，∴－2m2＋m＋3为偶数．...