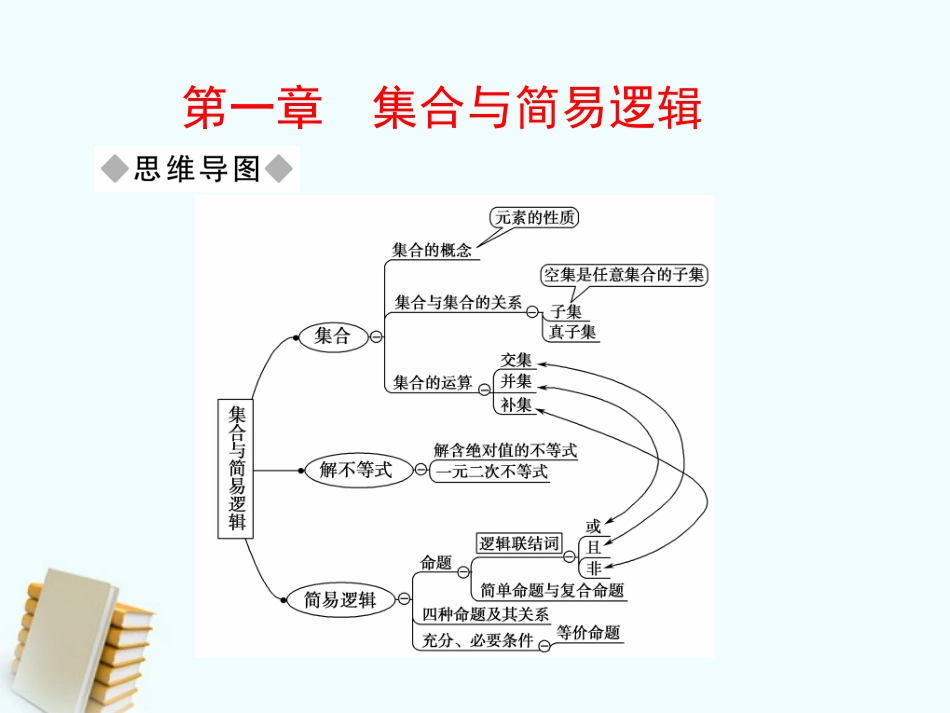
第一章集合与简易逻辑高考十分重视对本章内容的考查,多以选择题、填空题的形式考查集合之间的关系和集合的运算,通常与函数、不等式、方程等知识交汇在一起;简易逻辑主要考查四种命题及其关系、充要条件、逻辑联结词.通过本章的复习可以看到集合与简易逻辑是高中数学中的基础知识,在高中数学的各个部分都具有十分广泛的应用;是认识和使用数学语言的必备知识.第一节集合的概念与运算1.集合的基本概念(1)集合的概念:某些的对象集在一起就成为一个集合.(2)集合中元素的特性:、、.(3)集合的三种表示方法:、、.2.集合间的基本关系(1)子集:若集合A的都是集合B的元素,则A⊆B.(2)真子集:若A⊆B,且,则AB.(3)∅是任何集合的,是任何非空集合的.(4)相等:若A⊆B,且B⊆A,则A=B.指定确定性互异性无序性列举法描述法图示法任何一个元素A≠B子集真子集3.集合的基本运算补集交集并集符号表示若全集为U,则集合A的补集为∁UA图形表示意义∁UA={x|}{x|}{x|}A∩BA∪Bx∈U,且x∉Ax∈A,且x∈Bx∈A,或x∈B4.集合的常用运算性质(1)A⊆B⇔A∩B=⇔A∪B=.(2)∁U(A∩B)=;∁U(A∪B)=;(3)card(A∪B)=card(A)+card(B)-.AB(∁UA)∪(∁UB)(∁UA)∩(∁UB)card(A∩B)1.若给定集合A={x,4,x2},则集合A本身对实数x有限制条件吗?若有,请求出x的取值范围.【提示】由元素的互异性,可得解得x≠4,x≠±2,x≠0,x≠1.x≠4,x2≠4,x2≠x.2.如何区分数集与点集?下面三个集合:A={x|y=x2+1};B={y|y=x2+1},C={(x,y)|y=x2+1}是否是相同的集合?【提示】主要区分元素的属性,数集中的元素是“数”,而点集中的元素是有序实数对,集合A、B是数集,而集合C中的元素为有序实数对,可看成点集,实际上集合A、B可分别看成函数y=x2+1的定义域和值域.易知A=R,B={y|y≥1},三者不是相同集合,但BA.1.(教材改编题)设全集U={1,2,3,4},A={2,3},B={1},则A∩(∁UB)=________.【解析】 ∁UB={2,3,4},∴A∩(∁UB)={2,3}.【答案】{2,3}2.若x∈{1,x2},则实数x的值为________.【解析】当x=x2时,x=0或x=1,若x=1时,x2=1,由互异性知不符合题意;经检验知x=0符合题意.【答案】03.(2010·重庆高考)设A={x|x+1>0},B={x|x<0},则A∩B=___.【解析】 A={x|x>-1},B={x|x<0},∴A∩B={x|-1<x<0}.【答案】{x|-1<x<0}4.(2011·海淀模拟)已知集合A={x|-1≤x≤1},B={x|1-a≤x≤2a-1},若B⊇A,那么a的取值范围是________.【解析】由数轴知,【答案】a≥2设集合A={-1,1,3},B={a+2,a2+2},若B⊆A,则实数a的值为________.【思路点拨】由B⊆A知,集合B中的元素都属于集合A,又注意到a2+2≥2,故a2+2=3,解方程得出a的值后代入集合B检验是否符合题意.【尝试解答】 B⊆A,∴a2+2∈A,a+2∈A,∴a2+2=3,解得a=1或a=-1.当a=1时,B={3,3}不满足元素的互异性.当a=-1时,B={1,3},且满足B⊆A.故实数a的值为-1.【答案】-11.给定集合B后,已有a+2≠a2+2这一隐含条件,而在解题时我们若只注重用等量关系求a的值,而忽略元素的互异性,会导致增解,故此类问题,应将求得字母的值代入原集合,验证是否满足元素的互异性.2.本题的解答中利用a2+2=3求得a的值后,除检验互异性是否满足之外,还应检验B⊆A是否成立.因为a2+2=3只保证a2+2∈A,而不能保证a+2∈A.若将本例中的集合B改为B={a-2,a2+2},其他条件不变,则实数a的值为________.【解析】 B⊆A,∴a2+2∈A,a-2∈A∴a2+2=3,解得a=1或a=-1.当a=1时,B={-1,3},满足B⊆A.当a=-1时,B={-3,3},不满足B⊆A.故a=1.【答案】1已知集合A={x|y=-x2+3x-2},B={x|x2-(a+1)x+a≤0},且A⊆B,求实数a的取值范围.【思路点拨】思路二:求出集合A,利用A⊆B的定义,将问题转化为不等式恒成立问题.【尝试解答】法一由-x2+3x-2≥0得,1≤x≤2,∴A={x|1≤x≤2}.由x2-(a+1)x+a≤0,得(x-1)(x-a)≤0.①当a=1时,得x=1,故B={1};②当a>1时,得B={x|1≤x≤a};③当a<1时,得B={x|a≤x≤1}. A⊆B.∴得实数a的取值...