高中数学第三章空间向量与立体几何 小结与复习课件新课标人教A版选修2 课件VIP免费

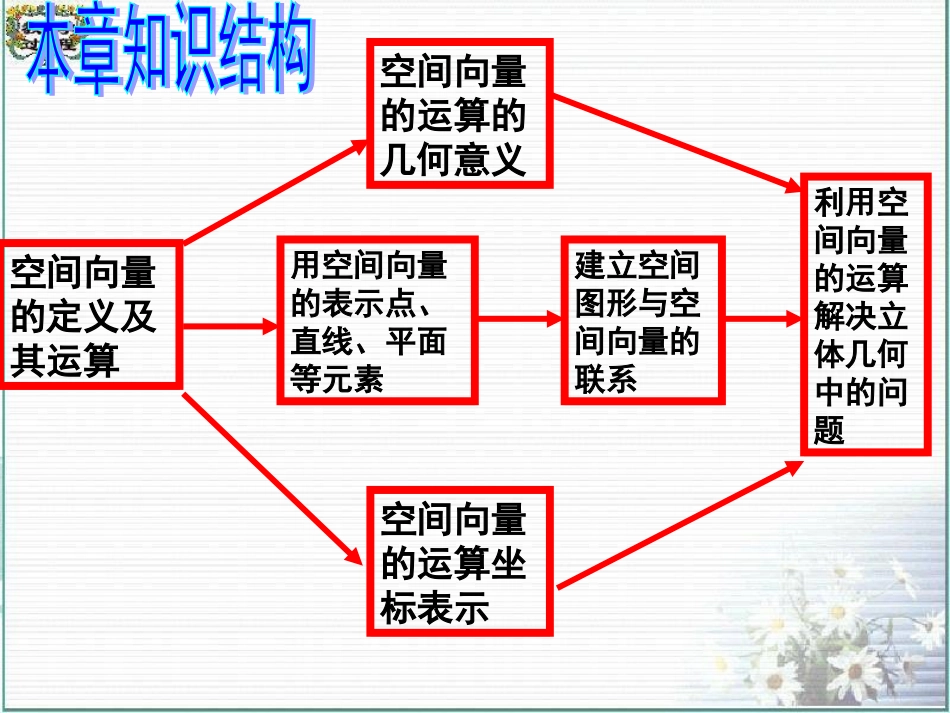
第三章空间向量与立体几何小结与复习空间向量的定义及其运算空间向量的运算的几何意义空间向量的运算坐标表示用空间向量的表示点、直线、平面等元素建立空间图形与空间向量的联系利用空间向量的运算解决立体几何中的问题归纳整理（一）基本概念（一）基本概念4.单位向量：模是1的向量。4.单位向量：模是1的向量。3.向量的模：向量的大小叫向量的长度或模。即表示向量的有向线段的长度。3.向量的模：向量的大小叫向量的长度或模。即表示向量的有向线段的长度。2.空间向量也用有向线段表示，并且同向且等长的有向线段表示同一向量或相等的向量．2.空间向量也用有向线段表示，并且同向且等长的有向线段表示同一向量或相等的向量．1.空间向量：空间中具有大小和方向的量叫做向量．1.空间向量：空间中具有大小和方向的量叫做向量．5.零向量：模是0的向量。零向量的方向是任意的。有向线段的起点与终点重合。5.零向量：模是0的向量。零向量的方向是任意的。有向线段的起点与终点重合。（一）基本概念（一）基本概念归纳整理7.相反向量：模相等且方向相反的向量叫做相反向量．7.相反向量：模相等且方向相反的向量叫做相反向量．6.相等向量：模相等且方向相同的向量叫做相等向量．6.相等向量：模相等且方向相同的向量叫做相等向量．8.如果表示空间向量的有向线段所在的直线互相平行或重合，则这些向量叫做共线向量或平行向量。9.平行于同一平面的向量，叫做共面向量n10.平面的法向量：如果表示向量的有向线段所在直线垂直于平面，则称这个向量垂直于平面,记作⊥，如果⊥，那么向量叫做平面的法向量.nnn(二)空间向量的运算1.加法:三角形法则或平行四边形法则2.减法:三角形法则abba加法交换律加法结合律()()abcabc注:两个空间向量的加、减法与两个平面向量的加、减法实质是一样的.三个向量或三个以上向量的和遵循空间多边形法则3.数乘向量运算。与平面向量一样,实数与空间向量a的乘积a仍然是一个向量.⑴当0时,a与向量a的方向相同;⑵当0时,a与向量a的方向相反;⑶当0时,a是零向量.（4）aa空间向量的数乘运算满足分配律及结合律();;()()ababaaaaa即：（）4、两个向量的数量积注:①两个向量的数量积是数量，而不是向量.②规定:零向量与任意向量的数量积等于零.空间两个向量的数量积的性质注：空间向量的数量积具有和平面向量的数量积完全相同的性质.1.共线向量定理:对空间任意两个向量的充要条件是存在实数使,(0),//abbabab2、平面向量基本定理如果e1和e2是一平面内的两个不平行的向量，那么，该平面内的任一向量a，存在惟一的一对实数a1，a2，使a＝a1e1＋a2e23.共面向量定理:如果两个向量ab、不共线,则向量p�与向量ab、共面的充要条件是存在唯一的有序实数对(,)xy使pxayb�.(三)空间向量的理论OABPa若P为A,B中点,则12�OPOAOB向量参数表示式共线向量定理的推论:如果为经过已知点A且平行已知非零向量的直线,那么对任一点O,点P在直线上的充要条件是存在实数t,满足等式其中向量叫做直线的方向向量.laalOPOAta�l若则A、B、P三点共线。OPOAtAB�()APtAB�或(1)OPxOAyOBxy�若，则A、B、P三点共线。（1）点P在平面上∴唯一有序实数对(,),xy使APxayb�①⑵ 已知点BC、在平面内且ABa�,ACb�∴点P在平面上是存在唯一有序实数对(,),xy使APxAByAC�②⑶ 已知点A、BC、在平面内且ABa�,ACb�,对于空间任意一点O∴点P在平面上是存在唯一有序实数对(,),xy使OPOAxAByAC�③（4）对于不共线的三点ABC、、和平面ABC外的一点O,空间一点P满足关系式OPxOAyOBzOC�,则点P在平面ABC内的充要条件是1xyz.共面向量定理的推论:4.空间向量基本定理若三个向量a，b，c不共面，则对空间任一向量p，存在有序实数组{x，y，z}，使得p＝xa＋yb＋zc.其中{a，b，c}叫做空间的一个基底，a，b，c都叫做基向量若空间向量的一个...