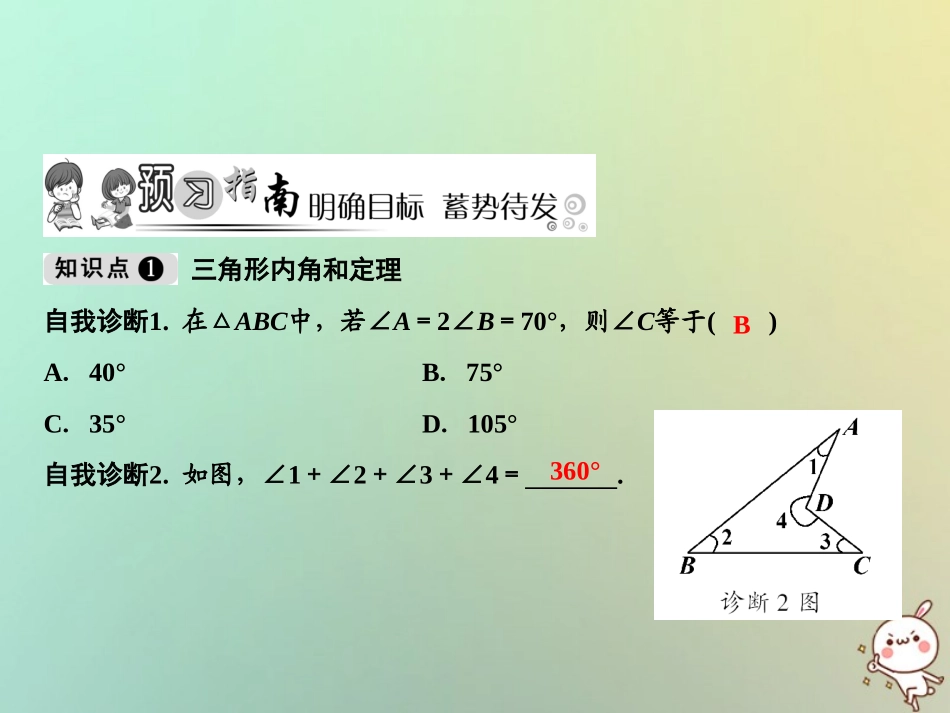
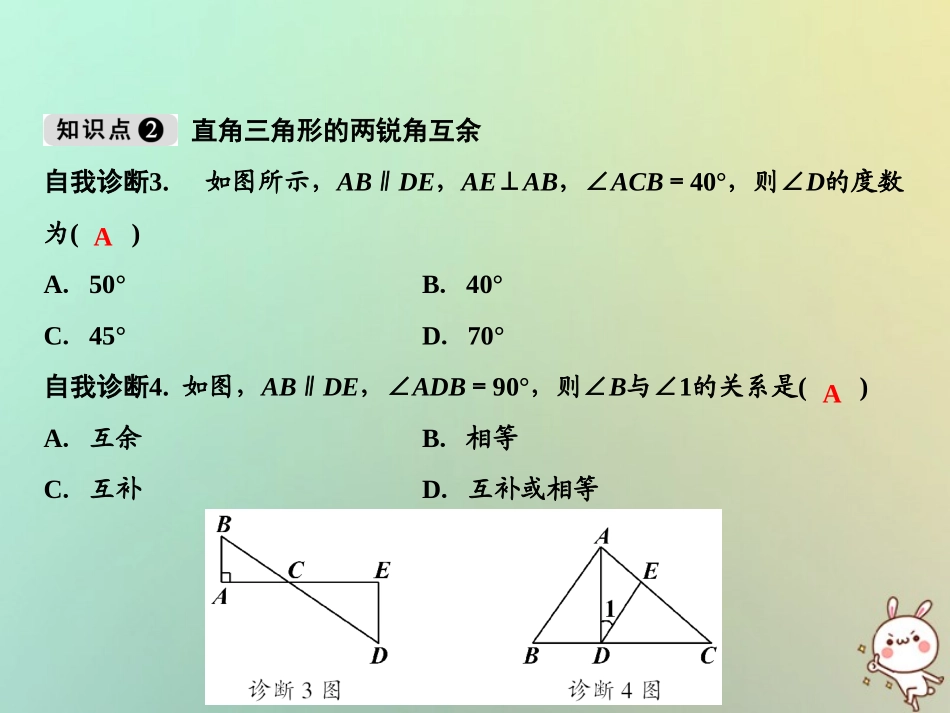
第13章三角形中的边角关系、命题与证明13.2命题与证明第3课时2018秋季数学八年级上册•HK三角形内角和定理自我诊断1.在△ABC中,若∠A=2∠B=70°,则∠C等于()A.40°B.75°C.35°D.105°自我诊断2.如图,∠1+∠2+∠3+∠4=.B360°直角三角形的两锐角互余自我诊断3.如图所示,AB∥DE,AE⊥AB,∠ACB=40°,则∠D的度数为()A.50°B.40°C.45°D.70°自我诊断4.如图,AB∥DE,∠ADB=90°,则∠B与∠1的关系是()A.互余B.相等C.互补D.互补或相等AA1.如图是赛车跑道的一段示意图,其中AB∥DE,测得∠ABC=140°,∠CDE=120°,则∠C的度数为()A.120°B.100°C.140°D.90°B2.如图,直线l1∥l2,且l1、l2被直线l3所截.∠1=∠2=35°,∠P=90°,则∠3=.55°3.如图,AD∥BC,AB∥CD,∠B=110°.延长AD至点F,延长CD至点E,连接EF,则∠E+∠F=.4.如图,AB∥CD,∠C=65°,CE⊥BE,垂足为E,则∠B的度数为.70°25°5.补充下列证明过程,并在括号里填上推理的依据.(1)已知:如图,△ABC.求证:∠A+∠B+∠C=180°;(2)证明:过点A作AD∥BC,则∠C=(),∠B+=180°(),即∠B+∠BAC+=180°.所以∠B+∠BAC+=180°().∠DAC∠DAB∠DAC∠C两直线平行,内错角相等两直线平行,同旁内角互补等量代换6.如图,AB⊥BC,AD⊥CD.求证:∠A+∠C=180°.证明:连接AC,在△ACD中,∵∠D=90°(已知),∴∠DAC+∠ACD=90°(直角三角形的两个锐角互余).在△ABC中,∵∠B=90°(已知),∴∠BAC+∠ACB=90°(直角三角形的两个锐角互余),∴∠DAC+∠ACD+∠BAC+∠ACB=∠A+∠C=180°(等式的性质).7.如图,∠ACB=90°,CD⊥AB,垂足为点D,下列结论错误的是()A.图中有三个直角三角形B.∠1=∠2C.∠1和∠B都是∠A的余角D.∠2=∠AB8.(大庆中考)在△ABC中,∠A、∠B、∠C的度数之比为2∶3∶4,则∠B的度数为()A.120°B.80°C.60°D.40°C9.如图,直线l1∥l2,l3⊥l4.有三个命题:①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4.下列说法中正确的是()A.只有①正确B.只有②正确C.①和③正确D.①②③都正确A10.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C=.11.如图,在△ABC中,∠A=60°,BO1、BO2是∠ABC的三等分线,CO1、CO2是∠ACB的三等分线,则∠BO1C=,∠BO2C=.20°140°100°12.在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数为.30°或60°13.如图,∠B=42°,∠A+10°=∠1,∠ACD=64°.求证:AB∥CD.解:∵∠A+10°=∠1,∠A+∠B+∠1=180°,∠B=42°,∴∠A+42°+∠A+10°=180°,∴∠A=64°.∵∠ACD=64°,∴∠A=∠ACD,∴AB∥CD.14.如图,D是△ABC的边BC延长线上的一点,DF⊥AB于点F,交AC于点E.∠A=40°,∠D=30°.求∠ACB的度数.证明:∵DF⊥AB,∴∠DFB=90°,∴∠B+∠D=90°.∵∠D=30°,∴∠B=60°.∵∠A=40°,∠A+∠B+∠C=180°,∴∠ACB=180°-∠A-∠B=80°.15.已知AD与BC相交于点O.(1)如图1,试探究∠A+∠B与∠C+∠D的数量关系;(2)若∠ABC和∠ADC的平分线相交于点E,如图2,试探究∠A、∠C、∠E之间的数量关系.解:(1)在△AOB中,∠A+∠B+∠AOB=180°,在△COD中,∠C+∠D+∠COD=180°,又∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D;(2)由(1)的结论可知∠A+∠ABE=∠E+∠ADE,∠C+∠CDE=∠E+∠EBC,∴∠A+∠ABE+∠C+∠CDE=∠E+∠ADE+∠E+∠EBC,又∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=∠EBC,∠ADE=∠CDE,∴∠A+∠C=2∠E.