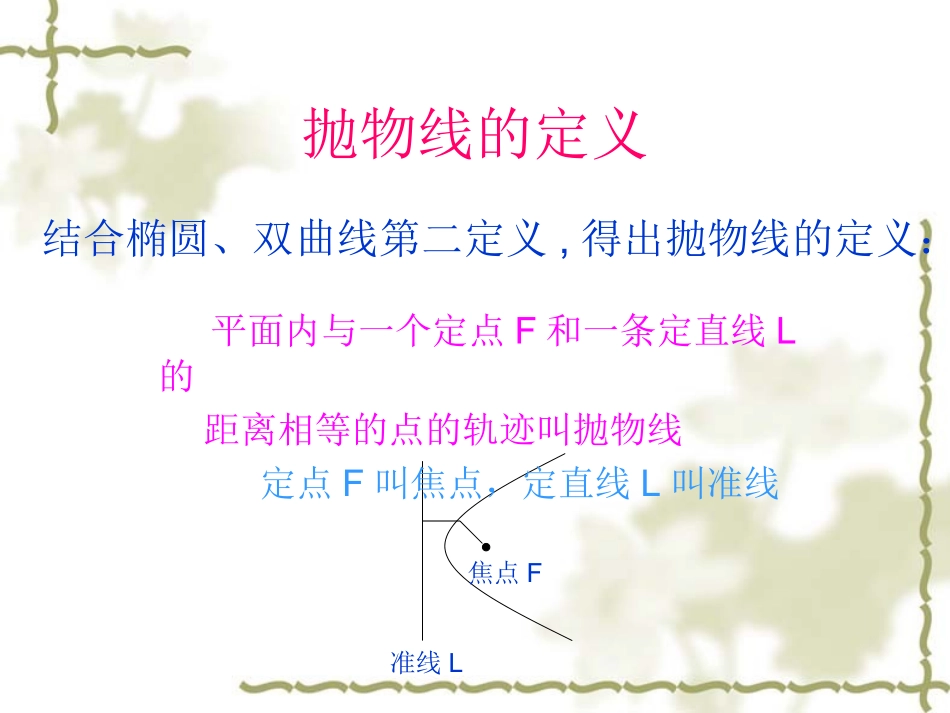
抛物线及其标准方程抛物线及其标准方程平面内与一个定点的距离和一条定直线的距离之比等于一个常数e的动点的轨迹:当01时轨迹是_________创设情景椭圆双曲线?当e=1时轨迹是_________抛物线的定义结合椭圆、双曲线第二定义,得出抛物线的定义:准线L焦点F平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫抛物线定点F叫焦点,定直线L叫准线由抛物线定义求标准方程求标准方程,前提要建立适当的坐标系LFLFLF123y2=2px+p2y2=2px–p2y2=2px抛物线的四种标准方程y2=2px(p>0)P为焦点到准线的距离表示如图顶点在原点,焦点为(,0),准线方程x=–的抛物线的标准方程.(即开口向右)开口向左:开口向上:开口向下:y2=–2px焦点(-,0)准线方程x=x2=2py焦点(0,)准线方程y=-x2=–2py焦点(0,-)准线方程y=LFxyoy=x四种抛物线标准方程的特点如何判断焦点在什么位置?看标准方程的一次项是x(y),则焦点在x(y)轴如果一次项系数为正,焦点在正半轴如果一次项系数为负,焦点在负半轴抛物线及其标准方程例1已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程.23解:(1)由题意知,2P=6,P=3,开口向右焦点坐标(,0),准线方程:x=-23抛物线及其标准方程例2:已知抛物线焦点坐标(0,-2),求它的标准方程.解:焦点在轴的负半轴,可设标准方程为:x2=-2py=2,p=4,即所求方程为x2=-8y2p抛物线及其标准方程随堂练习求下列抛物线方程的焦点坐标和准线方程(1)y2=8x(2)x2=4y(3)2y2+3x=0(4)6y=-x2焦点坐标(2,0),准线方程:x=-2焦点坐标(0,1),准线方程:y=-1焦点坐标(-3/8,0),准线方程:x=3/8焦点坐标(0,-3/2),准线方程:y=3/2抛物线及其标准方程例3:求经过点A(2,-3)的抛物线的标准方程32解:点A(2,-3)在第四象限,可设抛物线的标准方程为:y2=2px或X2=-2py把A(2,-3)代入y2=2px,得p=把A(2,-3)代入x2=-2py,得p=所求抛物线方程为:2y2=9x或3x2=-4y49抛物线及其标准方程练一练:求焦点到准线的距离为2的抛物线的标准方程.解:由题意知,抛物线的标准方程可设为:y2=2px或y2=-2px或x2=2py或x2=-2py因为p=2所以抛物线的标准方程是:y2=4x或y2=-4x或x2=4y或x2=-4y抛物线及其标准方程本课小结抛物线的定义:平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫抛物线.定点F叫抛物线的焦点,定直线L叫抛物线的准线.P为定点F到定直线L的距离.平面内到定点F和定直线L的距离之比等于常数e,当0<e<1时,轨迹为椭圆;当e=1时,轨迹为抛物线;当e>1时,轨迹为双曲线.这就是圆锥曲线的统一定义.抛物线的四种标准方程图象标准方程焦点坐标准线方程y2=2pxy2=–2pxx2=2pyx2=–2py(,0)(–,0)(0,)(0,–)X=–X=y=–y=抛物线及其标准方程作业:课本119页2,3,4