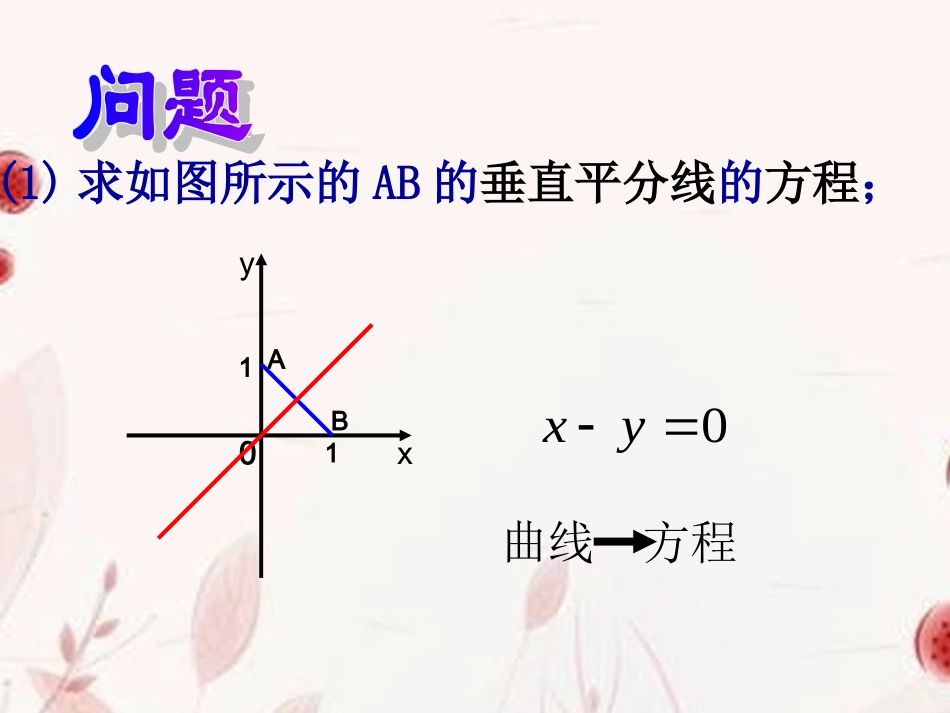
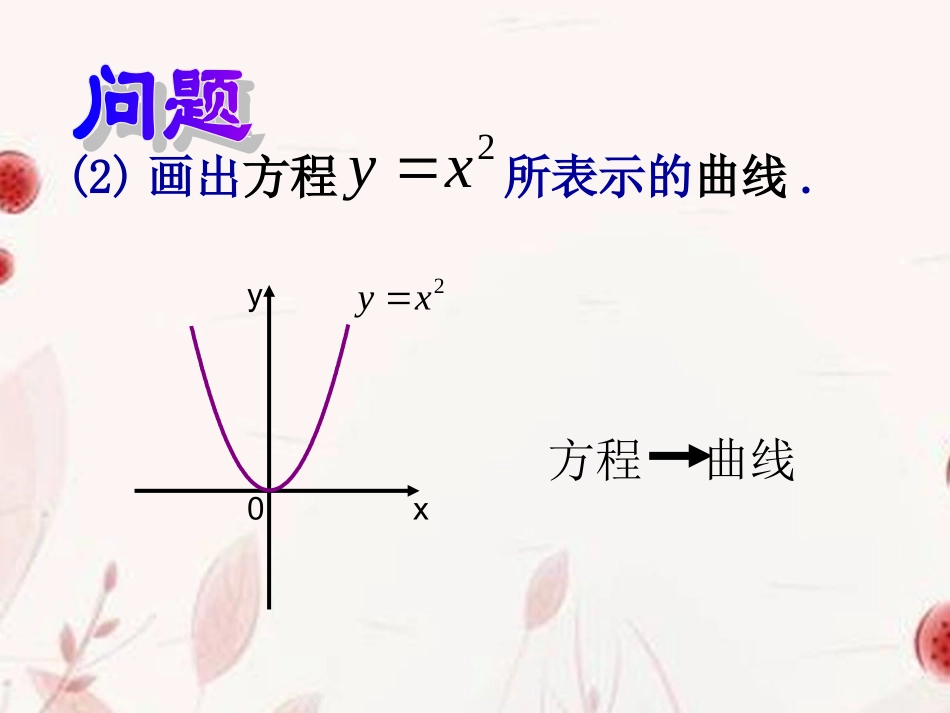
曲线与方程(一)曲线方程0xy(1)求如图所示的AB的垂直平分线的方程;110xyBA(2)画出方程所表示的曲线.2xy方程曲线2xy0xy(3)L是过点(0,1)且斜率为2的直线,能否说方程是直线的方程?为什么?)0(12xxy不能!(4)求轨迹方程的一般步骤是什么?(纯粹性)(完备性)F(x,y)=0曲线的方程与方程的曲线:⑴曲线上的点的坐标都是方程的解;⑵以方程的解为坐标的点都在曲线上;平面直角坐标系中,如果曲线C与方程之间具有如下关系:0),(yxF0),(yxF那么就说曲线C是方程的曲线,方程是曲线C的方程.0),(yxF0),(yxF0),(yxF8ͼ2-1-122xyO例1:判断下列命题是否正确解:(1)不正确,不具备(2)完备性,应为x=3,(2)不正确,不具备(1)纯粹性,应为y=±1.(3)正确.(4)不正确,不具备(2)完备性,应为x=0(-3≤y≤0).(1)过点A(3,0)且垂直于x轴的直线的方程为︱x︱=3(2)到x轴距离等于1的点组成的直线方程为y=1(3)到两坐标轴的距离之积等于1的点的轨迹方程为︱xy︱=1(4)ABC△的顶点A(0,-3),B(1,0),C(-1,0),D为BC中点,则中线AD的方程x=0例1变式:下列各题中,下图各曲线的曲线方程是所列出的方程吗?为什么?(1)曲线C为过点A(1,1),B(-1,1)的折线(如图(1))其方程为(x-y)(x+y)=0;(2)曲线C是顶点在原点的抛物线其方程为x+=0;(3)曲线C是Ⅰ,Ⅱ象限内到x轴,y轴的距离乘积为1的点集其方程为y=。10xy-110xy-11-2210xy-11-221y⑴⑵⑶不是不是是例2已知坐标满足方程的点都在曲线C上,那么下列说法正确的是()(A)曲线C上的点的坐标都满足方程;(B)凡坐标不满足方程的点都不在曲线C上;(C)不在曲线C上的点的坐标必不满足方程;(D)不在曲线C上的点的坐标有些满足方程,有些不满足方程.C(,)0fxy例2变式:若命题“曲线C上的点的坐标满足方程f(x,y)=0”是正确的,则下列命题中正确的是()A.方程f(x,y)=0所表示的曲线是CB.坐标满足f(x,y)=0的点都在曲线C上C.方程f(x,y)=0的曲线是曲线C的一部分或是曲线CD.曲线C是方程f(x,y)=0的曲线的一部分或是全部D例3证明与两条坐标轴的距离的积是常数k(k>0)的点的轨迹方程是xy=±k.证明(1)如图设M(x0,y0)是轨迹上任意一点,∵点M与x轴的距离为|y0|,与y轴的距离为|x0|,|x∴0||y0|=k,即(x0,y0)是方程xy=±k的解.(2)设点M1的坐标(x1,y1)是方程xy=±k的解,则x1y1=±k,即|x|.|y|=k,而|x1|,|y1|是点M1到y轴,x轴的距离,因此点M1到这两条直线距离积是常数k,点M1是曲线上的点.由(1)(2)知,xy=±k是与两条坐标轴距离的积为常数k(k>0)的点的轨迹方程.QRMyxO例4:两个定点的距离为6,点M到这两个定点的距离的平方和为26,求点M的轨迹方程答案:224xy第一步,设M(x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;归纳:证明已知曲线的方程的方法和步骤第二步,设(x0,y0)是f(x,y)=0的解,证明点M(x0,y0)在曲线C上.课堂练习:1:下述方程表示的图形分别是下图中的哪一个?①-=0xy|x|-|y|=0②③x-|y|=011OXY11OXY11OXY-1-111OXY-1ABCD①表示B②表示C③表示DC2:设圆M的方程为,直线l的方程为x+y-3=0,点P的坐标为(2,1),那么()2)2()3(22yxA.点P在直线上,但不在圆上B.点P在圆上,但不在直线上;C.点P既在圆上,也在直线上D.点P既不在圆上,也不在直线上3:已知方程的曲线经过点,则m=_____,n=______.0422nymx)1,2(),2,1(BA4545课堂练习:4.“曲线C上的点的坐标都是方程(,)fxy=0的解”是“方程(,)fxy=0是曲线C的方程”的()条件.(A)充分非必要(B)必要非充分(C)充要(D)既非充分也非必要5.△ABC的顶点坐标分别为(4,3)A,(2,1)B,(5,7)C,则AB边上的中线的方程为___________.B3210(1)xyx≤≤5本节课我们通过实例的研究,掌握了“曲线的方程”和“方程的曲线”的定义,在领会定义时,要牢记关系⑴、⑵两者缺一不可,它们都是“曲线的方程”和“方程的曲线”的必要条件,两者都满足了“曲线的方程”和“方程的曲线”才具备充分性。曲线和方程之间一一对应的确立,进一步把“曲线”与“方程”统一了起来,在此基础上,我们就可以更多地用代数的方法研究几何问题。再见