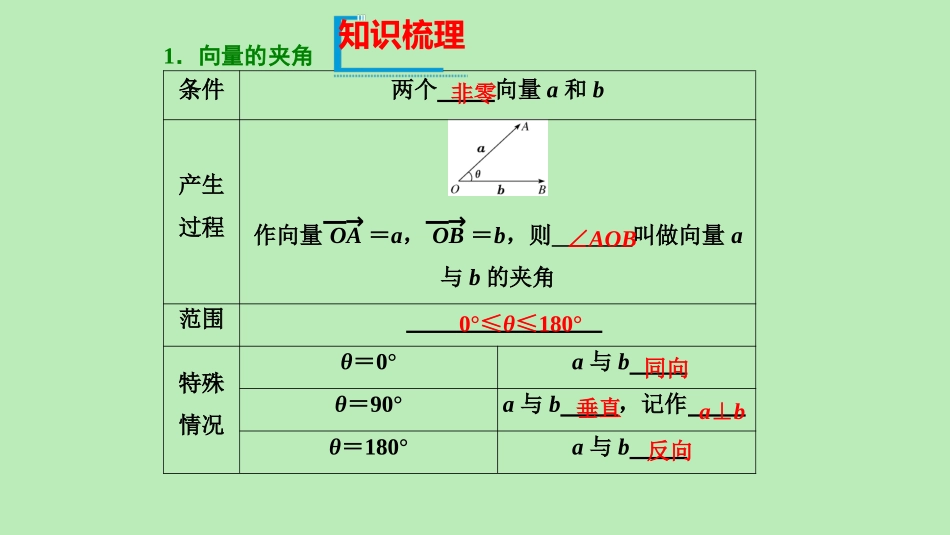
6.2.4向量的数量积学习目标1.通过物理中功等实例,理解平面向量的数量积的概念及其物理意义,会计算平面向量的数量积.2.通过几何直观,了解平面向量投影的概念以及投影向量的意义.3.会用数量积判断两个平面向量的垂直关系.重点:平面向量的数量积的概念及其应用.难点:对平面向量的数量积的概念的理解以及平面向量数量积的应用.1.向量的夹角条件两个向量a和b产生过程作向量OA―→=a,OB―→=b,则叫做向量a与b的夹角范围特殊情况θ=0°a与bθ=90°a与b,记作θ=180°a与b∠AOB同向垂直反向非零0°≤θ≤180°a⊥b知识梳理2.向量数量积的定义(1)两个非零向量的数量积:已知条件向量a,b是非零向量,它们的夹角为θ定义a与b的数量积(或内积)是数量记法(2)规定:零向量与任一向量的数量积均为0.|a||b|cosθa·b=|a||b|cosθ[点睛](1)两向量的数量积,其结果是数量,而不是向量,它的值等于两向量的模与两向量夹角余弦值的乘积,其符号由夹角的余弦值来决定.(2)两个向量的数量积记作a·b,千万不能写成a×b的形式.3.向量的数量积的几何意义设两个非零向量a,b,它们的夹角为θ.(1)投影的概念:①向量b在a的方向上的投影为.②向量a在b的方向上的投影为.(2)数量积的几何意义:数量积a·b等于a的长度|a|与的乘积.|b|cosθ|a|cosθb在a的方向上的投影|b|cosθ[点睛](1)b在a方向上的投影为|b|cosθ(θ是a与b的夹角),也可以写成a·b|a|.(2)投影是一个数量,不是向量,其值可为正,可为负,也可为零.4.向量数量积的性质设a与b都是非零向量,θ为a与b的夹角.(1)a⊥b⇔.(2)当a与b同向时,a·b=,当a与b反向时,a·b=.(3)a·a=或|a|=a·a=a2.(4)cosθ=.(5)|a·b||a||b|.a·b=0|a||b|[点睛]对于性质(1),可以用来解决有关垂直的问题,即若要证明某两个向量垂直,只需判定它们的数量积为0;若两个非零向量的数量积为0,则它们互相垂直.-|a||b||a|2a·b|a||b|≤5.向量数量积的运算律(1)a·b=(交换律);(2)(λa)·b==(结合律);(3)(a+b)·c=(分配律).b·aλ(a·b)a·c+b·c[点睛](1)向量的数量积不满足消去律:若a,b,c均为非零向量,且a·c=b·c,但得不到a=b.(2)(a·b)·c≠a·(b·c),因为a·b,b·c是数量积,是实数,不是向量,所以(a·b)·c与向量c共线,a·(b·c)与向量a共线,因此,(a·b)·c=a·(b·c)在一般情况下不成立.a·(λb)例1一平面向量数量积的计算1.向量数量积的基本计算常考题型已知|a|=6,|b|=5,当:(1)a∥b;(2)a⊥b;(3)a与b的夹角为60°时,分别求a与b的数量积.【解】(1)当a∥b时,若a与b同向,则θ=0°,a·b=|a||b|cos0°=6×5=30;若a与b反向,则θ=180°,a·b=|a||b|cos180°=-6×5=-30.(2)当a⊥b时,a与b的夹角为90°,a·b=|a||b|cos90°=0.(3)当a与b的夹角为60°时,a·b=|a||b|cos60°=6×5×12=15.【提示】平面向量数量积的计算方法(1)定义法利用定义中的公式a·b=|a||b|cosθ求数量积.(2)利用运算律转化法根据数量积的运算律,由(a+b)·(c+d)=a·c+a·d+b·c+b·d可得如下运算公式:(a+b)·(a-b)=|a|2-|b|2;(a+b)2=|a|2+2a·b+|b|2;(a-b)2=|a|2-2a·b+|b|2.(3)利用向量的线性运算转化法涉及平面图形中向量的数量积的计算时,要结合向量的线性运算,将未知向量转化为已知向量求解.训练题1.2.[2019·兰州一中高一期末]已知平面向量a,b的夹角为23,|a|=1,|b|=2,则a·(a+b)=()A.3B.2C.0D.1+3[2019·辽宁本溪市高级中学高一检测]已知|a|=5,|b|=2,向量a与b的夹角θ=60°,求(a+2b)·(a-3b).C解:因为|a|=5,|b|=2,向量a与b的夹角θ=60°,∴a·b=|a|·|b|·cos〈a,b〉=5×2×12=5,∴(a+2b)·(a-3b)=a2-a·b-6b2=25-5-24=-4,故(a+2b)·(a-3b)=-4.例22.几何图形中的数量积[2019·广东深圳市高级中学高三模拟]已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则AF�·BC�的值为()A.-58B.118C.14D.18【解析】由DE=2EF,可得DE�=2EF�,EF�=12DE�,如图,连接AE,则...