高中数学 向量的加法比赛课件VIP免费

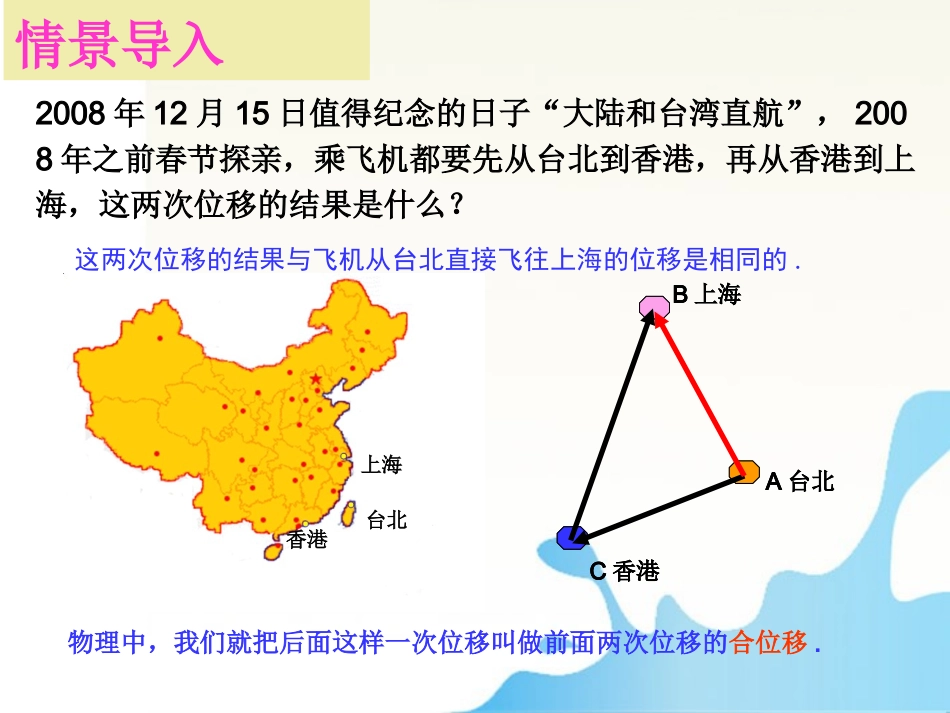
(><)O三角形法则平行四边形法则(><)O2、从位移的合成到向量的加法§2.1.1向量的加法2、什么叫相等向量？1、什么叫向量？如何表示？3、什么叫平行向量（共线向量）？既有大小，又有方向的量叫做向量.有向线段方向相同，长度相等的两个向量叫做相等向量.两个向量的有向线段所在的直线平行或重合,则称这两个向量平行或共线.2008年12月15日值得纪念的日子“大陆和台湾直航”，2008年之前春节探亲，乘飞机都要先从台北到香港，再从香港到上海，这两次位移的结果是什么？B上海C香港A台北上海台北香港物理中，我们就把后面这样一次位移叫做前面两次位移的合位移.这两次位移的结果与飞机从台北直接飞往上海的位移是相同的.B上海C香港A台北情景导入AB在大型车间里,一重物被天车从A处搬运到B处.它的实际位移AB,可以看作水平运动的分位移AC与竖直向上运动的分位移AD的合位移.CD什么叫两个向量的和向量？位移就是一个向量，两个位移求和位移实际上就是两个向量求和向量。如何求ab?1.向量加法的定义:,abab,ab我们把求两个向量的和的运算，叫做向量的加法，叫做的和向量。AC2.它们之间有联系吗?1.两种方法做出的结果一样吗?向量加法的定义任意给出两个向量a与b.如何求a+b.ababBa+babBOACa+bAB+BC=ACbbaba三角形法则:平行四边形法则:AC2.它们之们有联系吗?1.两种方法做出的结果一样吗?向量加法的定义任意给出两个向量a与b.如何求a+b.ababBa+babBOACa+bb向量加法的三角形法则:1.将向量平移使得它们首尾相连.2.和向量即是第一个向量的起点指向第二个向量的终点.向量加法的平行四边形法则:1.将向量平移到同一起点.2.和向量即以它们作为邻边平行四边形的共起点的对角线.ababa+bbaa+b2.向量的加法法则首尾相连同一起点跟踪练习1、根据图形填空ABCDabc(2)+=cbDACBO(1)+=addE(3)+=abOE变式训练1、CABDECBDCEDAE:求CBDCADCBACAB向量加法的推广对于n-1个向量的和，若以空间中任意点为起点，连续作出这n-1个向量，使得它们依次首尾相接，则以第一个向量的起点为起点，最后一个向量的终点为终点的向量就是这n-1个向量的和．即12233411nnnAAAAAAAAAA�探究1：变式训练1、CABDECBDCEDAE:求CBDCADCBACABBACBDCEDAE:求变式训练2、0ABBCCAACCA�零向量思考：如果平面内有n个向量依次首尾连接组成一条封闭折线,那么这n个向量的和是什么?探究2：共线向量的加法：ABCCBA2、方向相反ba1、方向相同abAC=a+bAC=a+baaa:00注三角形法则加法交换律：abba)()(cbacbaBbacbacbbcD加法结合律：abbaOCBAbaAaCADCDBCAB结论：3：.向量的加法的运算律例1在小船过河时,小船沿垂直河岸方向行驶的速度为v1=km/h,河水流动的速v2=2.0km/h求小船过河实际航行速度.23知识拓展与应用ABDCP76练习1,2,4题)()(cbacba1、平行四边形法则：起点相同适用于不共线向量的加法2、三角形法则：首尾相接适用于任意向量的加法不共线向量交换律abba结合律任意向量3、运算律：P791、3题选做题如图，平面内有三个向量OCBAOCOBOA其中OBOA的夹角为，120OCOA的夹角为，301OBOA32OC若求ROBOAOC