高中数学 第三章(不等式)一元二次不等式的解法(二)课件 北师大版必修5 课件VIP免费

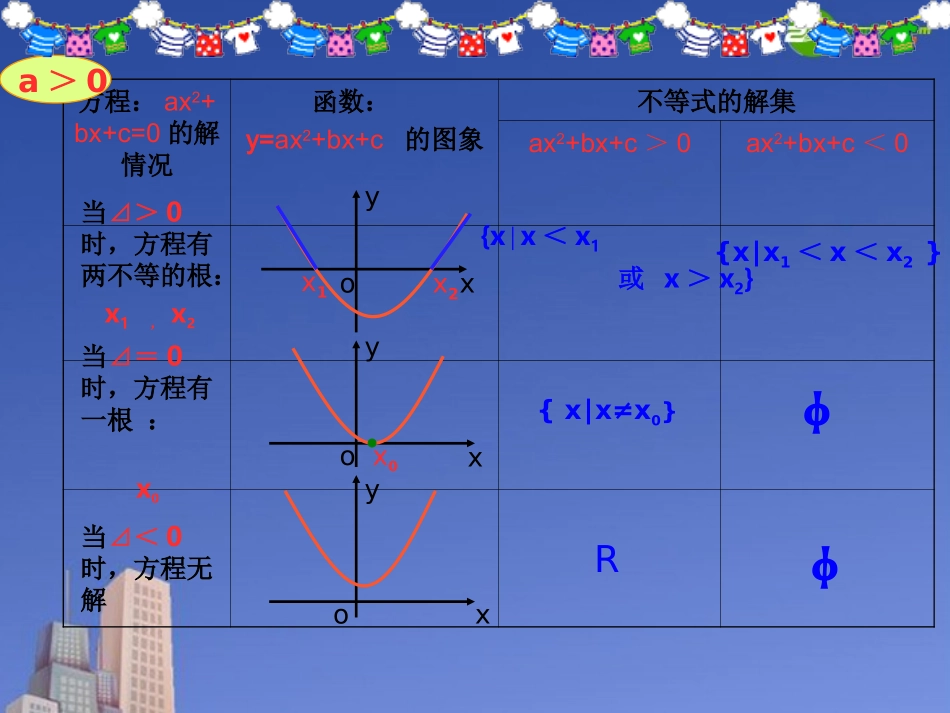
北师大版高中数学必修5第三章《不等式》一、教学目标：1．知识与技能：理解一元二次方程、一元二次不等式与二次函数的关系，掌握图象法解一元二次不等式的方法；培养数形结合的能力培养分类讨论的思想方法，培养抽象概括能力和逻辑思维能力；2．过程与方法：经历从实际情境中抽象出一元二次不等式模型的过程和通过函数图象探究一元二次不等式与相应函数、方程的联系，获得一元二次不等式的解法；3．情态与价值：激发学习数学的热情，培养勇于探索的精神，勇于创新精神，同时体会事物之间普遍联系的辩证思想。二、教学重点：从实际情境中抽象出一元二次不等式模型；一元二次不等式的解法。教学难点：理解二次函数、一元二次方程与一元二次不等式解集的关系。三、教学方法：探析归纳，讲练结合四、教学过程方程：ax2+bx+c=0的解情况函数：y=ax2+bx+c的图象不等式的解集ax2+bx+c＞0ax2+bx+c＜0a＞0xyox1x2xox0yxoy当⊿＞0时，方程有两不等的根：x1，x2当⊿＝0时，方程有一根：x0当⊿＜0时，方程无解{x∣x＜x1或x＞x2}{x∣x≠x0}R{x∣x1＜x＜x2}φφ练习：222(1)220(2)340(3)2350xxxxxxR5{|1}2xx由以上例子归纳出解一元二次不等式的步骤：先将一元二次不等式二次项系数化为正数；解对应的一元二次方程；根据方程的根和不等号方向写出解集；解不等式组①{x+4>0x－１>0②{x+4<0x－１<0x+4<0x－１>0③{求不等式组的解集，就是将每一个不等式的解集求出来，取他们的公共部分即他们的交集。④{x+4>0x－１<01、一元二次不等式（x+a）（x+b）<0的解法解不等式（x+4）（x－１）<0方法一：用上节课所学的内容来解方法二：利用符号原则：x+4<0x－１>0①{②{x+4>0x－１<0解①得x∈解②得－40②（3x+1）（4x－7）≤0{|2,x<-3}xx或17{|}34xx例2、①（x－a）（x－b）<0（b>a）｛x｜a0）的解法有两种：①利用图象来解；②先化为一元一次不等式组来解；2、分析不等式的解法0xaxb例3、解不等式307xx①{x－３>0x＋７>0②{x－３<0x＋７<0或解：∴原不等式的解集为｛x｜x>3或x<－7｝练习：①②307xx2112xx{x｜x≥3或x<－7｝{x｜x>－1或x<－2｝问题：①（x－3）（x＋7）>0与的解集有何关系？（x－3）（x＋7）>0与的解集有何关系？307xx307xx307xx②（x－3）（x＋7）≥0与的解集有何关系？（x－3）（x＋7）≤0与的解集有何关系？307xx0()()0xaxaxbxb结论：⑴0()()0xaxaxbxb⑵⑶0{xaxb()()00xaxbxb⑷0{xaxb()()00xaxbxb1、对于xR∈，恒成立，求k的取值范围。2(2)0kkxkx2、⑴⑵106xx7261xx23k{|16}xx{|1,8}xxx或课时小结：进一步熟练掌握一元二次不等式的解法；一元二次不等式与一元二次方程以及一元二次函数的关系。作业布置：课本第89页的习题3.2[A]组第3、5题五、教后反思：