高中数学 231平面向量基本定理课件 新人教A版必修4 课件VIP免费

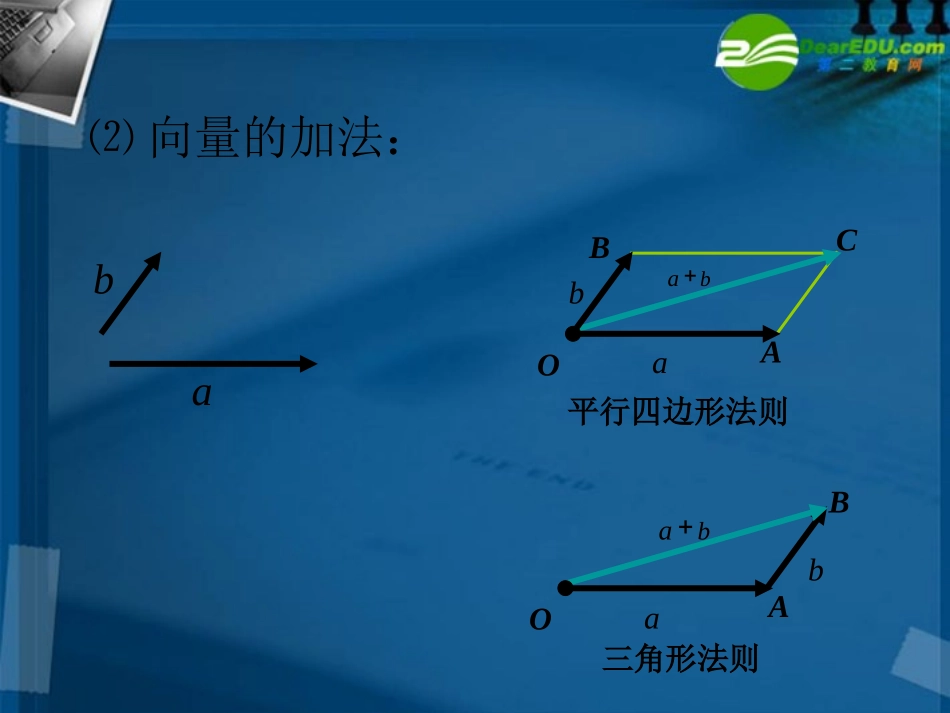
ba向量与非零向量共线的充要条件是当时，0与同向，ba且是的倍;||b||a当时，0与反向，ba且是的倍;||b||a||当时，00b，且。||0b1.复习:.ba有且只有一个实数，使得⑴向量共线充要条件ab⑵向量的加法：OBCAabOAaBbbaba平行四边形法则三角形法则1e�2e�OCABMNOCOMON�如图111OMOAe�1122OCee�1122+aee��即222ONOBe�a12eea�思考：一个平面内的两个不共线的向量、与该平面内的任一向量之间的关系.1e�2e�OCABMNaOCOMON�如图111OMOAe�1122OCee�1122+aee��即222ONOBe�1122+aee��1122+aee�这就是说平面内任一向量都可以表示成的形式平面向量基本定理：12121122+eeaaee���如果、是同一平面内的两个线的向量，那么对于这一平面内的任一向量，有且只有一对实数、，可使不共12ee�这里不共线的向量、叫做表示这一平面内所有向量的一组基底.1212,3.eeee�例1：已知向量（如图），求作向量-2.5作法:1e�2e�OA2..OACB作BC1e�-2.51.O如图，任取一点23e�1,2.5OAe�作OC�则，就是所求的向量2,3.OBe�2:,.ABCDMABaADbabMAMBMCMD�例如图，的两条对角线相交于点且，，用、表示、、和BACDABCDACABADabDBABADab��解：在中，M122221222212221222ababMAACababMBDBabMCACMAabMDDBMB����ab,.()ABCDACaBDbABADab��1.在中，设,则,用、来表示练习:1212122;;eeeeee���2.如图，已知向量、，求作下列向量:(1).3(2).41e�2e�2ab2abBACD112212121122112212121122121200AaaeeBeeCaaeeDeeee�.对平面中的任一向量，使的实数、有无数对.对实数、，不一定在平面内.空间任一向量可以表示为，这里、是实数.若实数、使则3.如果、是平面内所有向量的一组基底，那么（）,D小结:平面向量基本定理建议:预复习课本P105~108