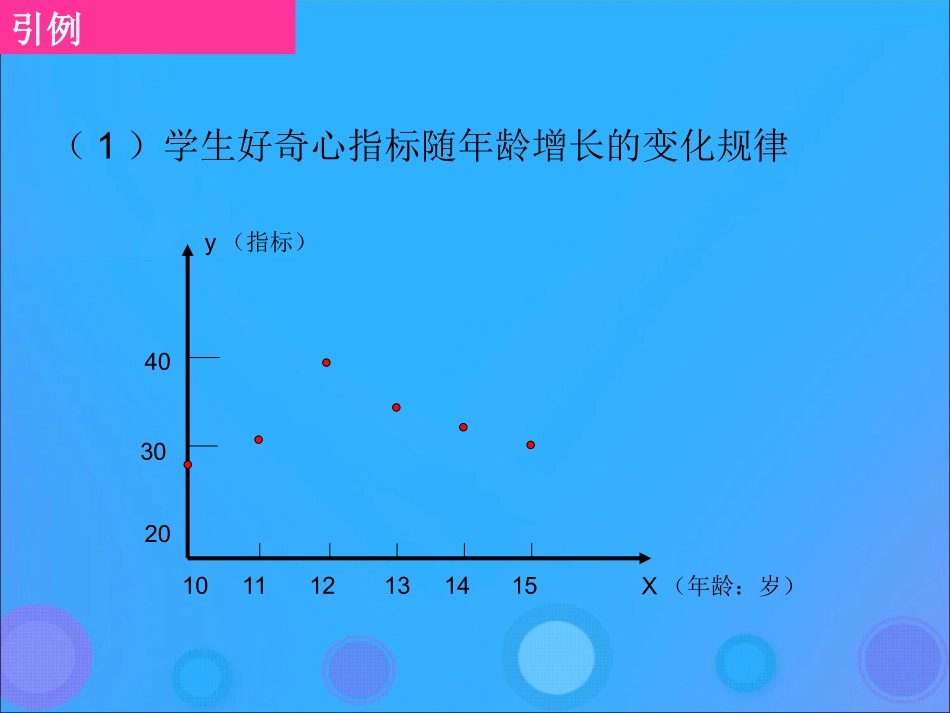
第二章函数2.1.1函数(一)—变量与函数的概念1.初中所学的函数的概念是什么?在一个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定唯一的一个y值,那么就称y是x的函数,其中x是自变量,y是因变量.2.初中学过哪些函数?正比例函数、反比例函数、一次函数、二次函数等.引例(1)学生好奇心指标随年龄增长的变化规律X(年龄:岁)304020101211131415y(指标)(2)玉米生长的各时间段与植株高度之间的相关数据4010020O821214Xy株高/cm生长阶段46102422201816262830326080180160140120200(4)电路中的电压U=220V,电流I与电阻R之间的变化规律。用欧姆定律表示,即UIR>0)R(总结:在上述的每个例子中,都指出了自变量的变化范围、由自变量确定因变量的对应法则,以及由此确定的因变量的取值范围一个函数关系必须涉及到两个数集和一个对应法则,实际上表达两个数集的元素之间,按照某种法则确定的对应关系,这反映了函数的本质思考:从集合与对应的观点分析,函数可以怎样定义?设集合A是一个非空的数集,对A中的任意数x,按照确定的法则f,都有唯一确定的数y与它对应,则这种对应关系叫做集合A上的一个函数.记作:y=f(x),xA其中x叫做自变量,自变量的取值范围(数集A)叫做这个函数的定义域。一、形成概念一、形成概念1.定义如果自变量取值a,则由法则f确定的值y称为函数在a处的函数值,记作:y=f(a)或y|x=a所有函数值构成的集合{y|y=f(x),x∈A}叫做这个函数的值域。函数y=f(x)也经常写作函数f或函数f(x)二、函数的二要素:定义域A;对应法则f.说明:说明:(1)函数符号y=f(x)表示y是x的函数,f(x)不是表示f与x的乘积;(3)“y=f(x)”是函数符号,可以用任意的字母表示,如:“y=g(x)”;(2)f表示对应法则,不同函数中f的具体含义不一样;abRa