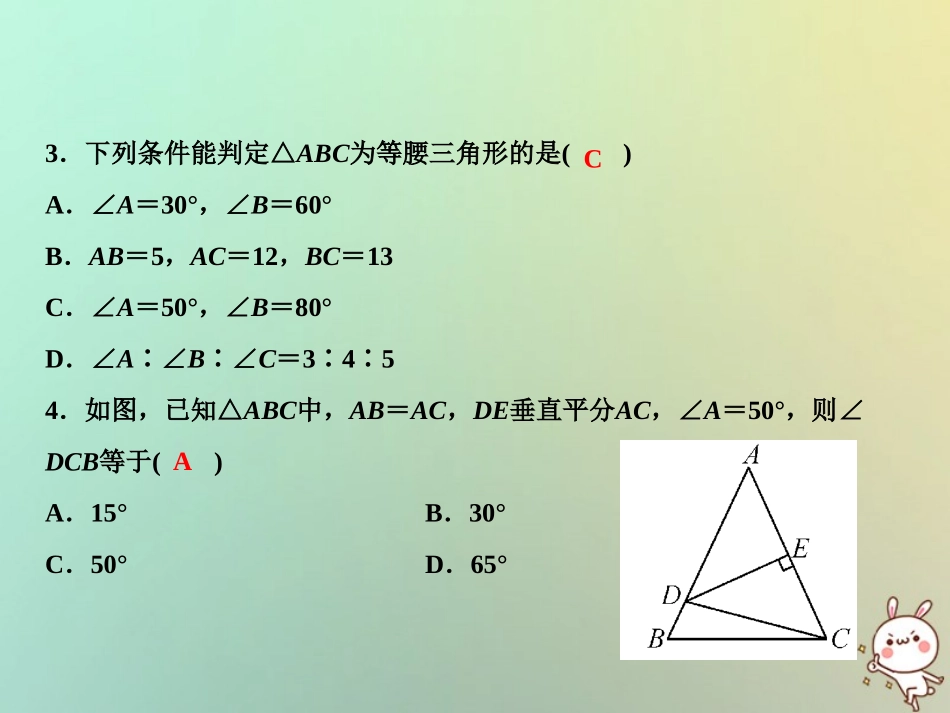
双休自测八(15.3~15.4)(时间:45分钟满分:100分)2018秋季数学八年级上册•HK一、选择题(4分×8=32分)1.若等腰三角形中有一个角等于66°,则这个等腰三角形的顶角的度数是()A.66°B.48°C.66°或57°D.66°或48°2.如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB度数为()DCA.70°B.55°C.40°D.35°3.下列条件能判定△ABC为等腰三角形的是()A.∠A=30°,∠B=60°B.AB=5,AC=12,BC=13C.∠A=50°,∠B=80°D.∠A∶∠B∶∠C=3∶4∶54.如图,已知△ABC中,AB=AC,DE垂直平分AC,∠A=50°,则∠DCB等于()A.15°B.30°C.50°D.65°CA5.如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作MN∥BC,分别交AB、AC于点M、N,若AB=12,AC=18,BC=24,则△AMN的周长为()A.30B.36C.39D.42A6.在△ABC中,已知∠A=∠B,且该三角形的一个内角等于100°.现有下面四个结论:①∠A=100°;②∠C=100°;③AC=BC;④AB=BC.其中正确的结论有()A.1个B.2个C.3个D.4个7.(河北中考)如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M、N分别在OA、OB上,且△PMN为等边三角形,则满足上述条件的△PMN有()A.1个B.2个C.3个D.3个以上BD8.(泰安中考)如图,在△PAB中,PA=PB,M、N、K分别是PA、PB、AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为()A.44°B.66°C.88°D.92°D二、填空题(4分×4=16分)9.已知等腰三角形的底边长为10cm,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长5cm,那么这个三角形的腰长为cm.10.如图,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D,则∠DBC=.1530°11.如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D,按此做法进行下去,∠DA3A的度数为.20°12.如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路:如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.(1)判定△ABD与△AED全等的依据是;(2)∠ACB与∠ABC的数量关系为:.SAS∠ACB=2∠ABC三、解答题(共52分)13.(8分)等腰三角形的周长为30cm,若底边长为xcm,腰长为ycm,写出y与x的关系式,并注明自变量的取值范围.解:由已知得y与x的关系式为x+2y=30,即y=-12x+15,自变量的取值范围是:0<x<15.14.(8分)如图,在Rt△ABC的斜边AB上取两点D、E,使AD=AC,BE=BC.当∠B=60°时,求∠DCE的度数.解: ∠ACB=90°,∠B=60°,∴∠A=30°. AD=AC,∴∠ACD=∠ADC=12(180°-∠A)=75°. BC=BE,∠B=60°,∴△BCE是等边三角形,∴∠BCE=60°,∴∠DCE=∠ACD+∠BCE-∠ACB=75°+60°-90°=45°.15.(10分)如图所示,104国道OA和327国道OB在曲阜市相交于O点,在∠AOB的内部有工厂C和D,现要建一个货站P,使P到OA和OB的距离相等,且使PC=PD,作出点P的位置(要求尺规作图,不写作法,保留作图痕迹).解:如图所示,点P即为所求.16.(12分)如图,已知△ABC中,∠C=90°,∠A=30°,DE垂直平分AB交AB于点D,交AC于点E,EC=2.求AE的长.解:连接BE. ED垂直平分AB,∴AE=BE,∴∠ABE=∠A=30°, ∠ABC=90°-30°=60°,∴∠EBC=60°-30°=30°,∴BE=2CE=2×2=4.∴AE=4.17.(14分)(1)如图①,∠B=∠D=90°,E是BD的中点,AE平分∠BAC,求证:CE平分∠ACD;(2)如图②,AM∥CN,∠BAC和∠ACD的平分线交于点E,过点E作BD⊥AM,分别交AM、CN于B、D,请猜想AB、CD、AC三者之间的数量关系,请直接写出结论,不要求证明;(3)如图③,AM∥CN,∠BAC和∠ACD的平分线交于点E,过点E作不垂直于AM的线段BD,分别交AM、CN于B、D,且B、D两点都在AC的同侧,(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.(1)证明:如图①,过E作EF⊥AC于F. ∠B=90°,AE平分∠BAC,∴EF=BE. E是BD的中点,∴BE...