高中数学 第一章 解三角形 正弦定理课件 新人教B版必修5 课件VIP免费

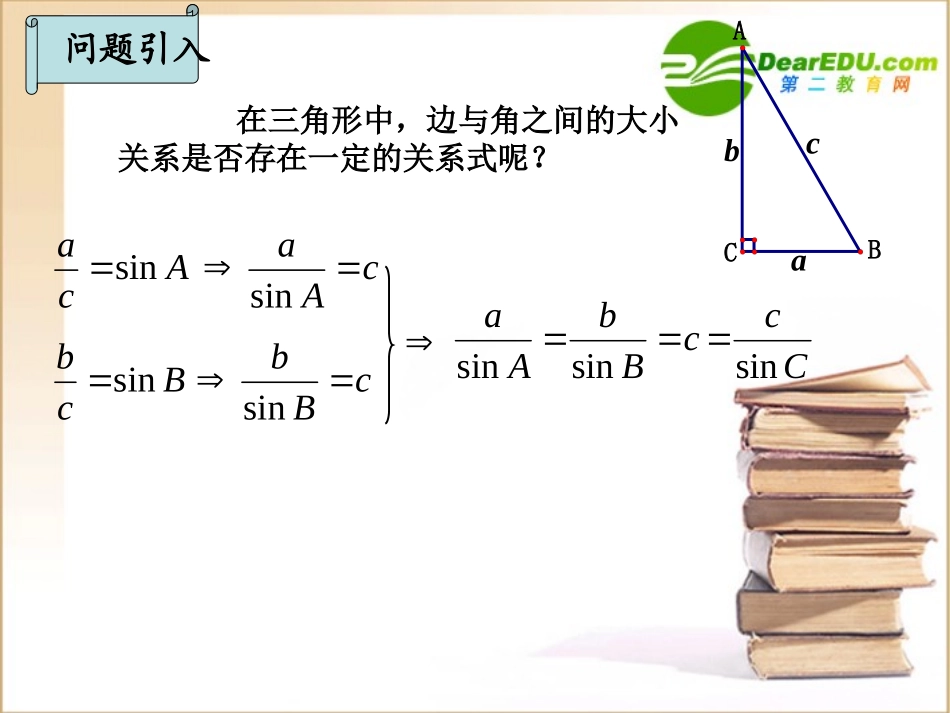
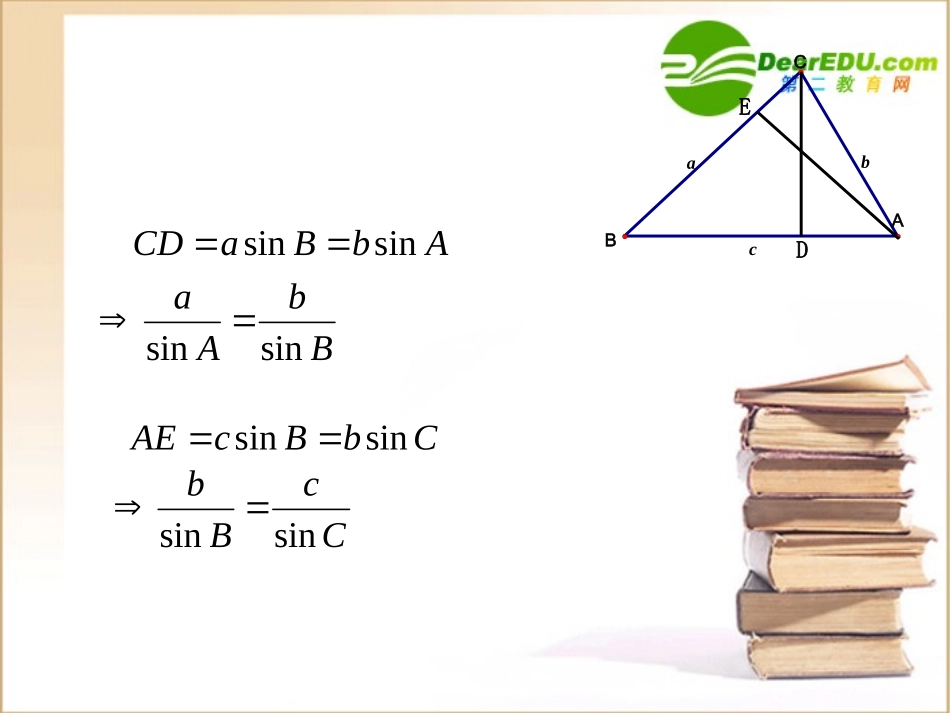
正弦定理（一）AcasinBcbsincAasincBbsincBbAasinsinaABCbcCcsin问题引入在三角形中，边与角之间的大小关系是否存在一定的关系式呢？acbCBADAbBaCDsinsinBbAasinsinECbBcAEsinsinCcBbsinsin在一个三角形中，各边和它所对角的正弦的比相等，即sinsinsinabcABC(0)kk正弦定理::sin:sin:sinabcABC练习1、在△ABC中，一定成立的等式是（）A、B、C、D、BbAasinsinBbAacoscosAbBasinsinAbBacoscos2、在△ABC中，下列关系中一定成立的是（）A、B、C、D、AbasinAbasinAbasinAbasinCD解三角形一般地，把三角形的三个角A、B、C和它们的对边a、b、c叫做三角形的元素，已知三角形的几个元素求其他元素的过程叫做解三角形。思考：利用正弦定理可以解决一些怎样的解三角形问题呢？⑴已知三角形的任意两个角与一边；A+B+C=180°C=180°-(A+B)⑵已知三角形的任意两边与其中一边的对角；例题⑴已知三角形的任意两个角与一边；例1、已知在△ABC中，b=12，A=30°，B=120°，解三角形。解：根据三角形内角和定理，C=180°-(A+B)=30°由正弦定理得CcBbAasinsinsin34120sin30sin12sinsinBAba同理，34ac练习21、（2005，北京文，5分）在△ABC中,,A=45°,B=75°,则BC的长为_____.3AC解：根据三角形内角和定理，B=180°-(A+C)=105°由正弦定理得CcBbAasinsinsin21030sin45sin10sinsinCAca6525sinsinCBcb例2、45,30,10ACcABC中，，解三角形。例题⑴已知三角形的任意两个角与一边；练习2、在△ABC中,A=60°,B=45°,c=20,解三角形。C=75°610230a)13(20b例题解：由正弦定理得CcBbAasinsinsin22sinsinaAbB⑵已知三角形的任意两边与其中一边的对角；例3、已知在△ABC中，，A=60°，则B=_____.24,34ba又a>b,所以A>B，所以B=45°45°例题解：由正弦定理得CcBbAasinsinsin23sinsinaAbB⑵已知三角形的任意两边与其中一边的对角；例4、已知在△ABC中，，A=45°，则B=_____.32,22ba又a1CAaAbBsinsin⑶sinB<1)sin(AbabaBAbaBA有二解有一解aababbbB2、A为直角或钝角时ba有一解无解ba练习：2、在△ABC中，a=x,b=2,B=45°,若这个三角形有两个解，则x的取值范围是_______.1、在△ABC中，a=2,b=6,A=30°,则此三角形的解（）A、有一个B、有两个C、没有D、无法确定C222x小结正弦定理用途：解斜三角形1.已知两角和任一边，求其它两边和一角；2.已知两边及其中一边对角，求另一边的对角及其他的边和角。2、在△ABC中，若，则B等于（）A、30°B、60°C、30°或150°D、60°或120°Abasin23Da23