高中数学 421直线与圆的位置关系课件2 新人教A版必修2 课件VIP免费

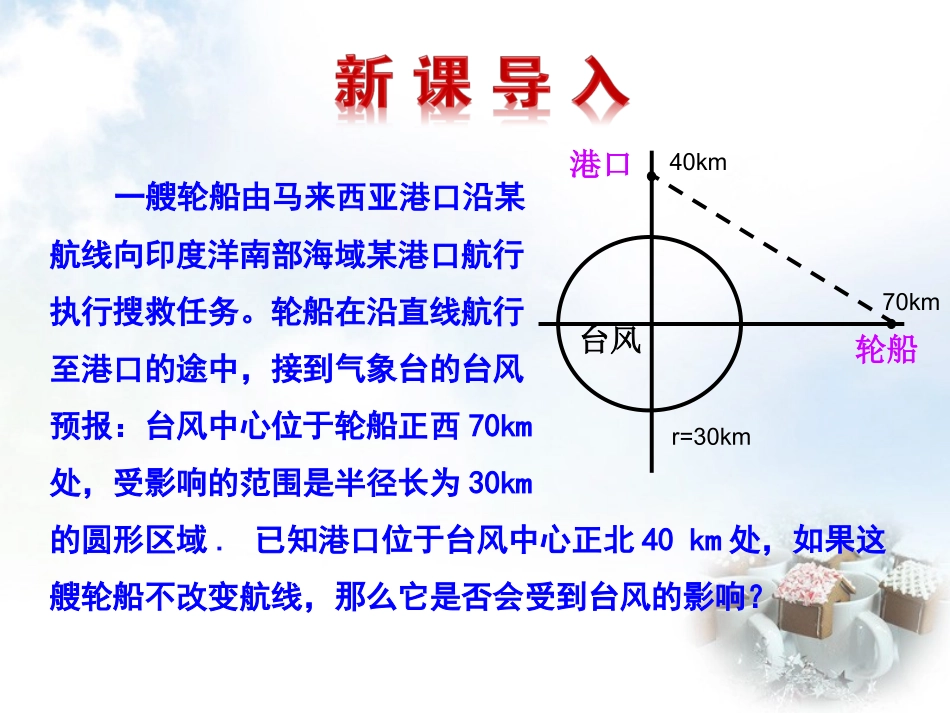
点到直线的距离公式，圆的标准方程和一般方程分别是什么？222()()xaybr22220(40)xyDxEyFDEF0022||AxByCdAB一艘轮船由马来西亚港口沿某航线向印度洋南部海域某港口航行执行搜救任务。轮船在沿直线航行至港口的途中，接到气象台的台风预报：台风中心位于轮船正西70km处，受影响的范围是半径长为30km的圆形区域.已知港口位于台风中心正北40km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？轮船港口台风40km70kmr=30km下面我们以月亮的起落为例.以蓝线为水平线,圆圈为月亮!注意观察!!一，直线与圆的位置关系的几种情况：．o圆心O到直线l的距离dl半径r1.直线l和⊙O相离,此时d与r大小关系为_________d>rl．o圆心O到直线l的距离d半径r2.直线l和⊙O相切,此时d与r大小关系为_________d=r．o圆心O到直线l的距离d半径r3.直线l和⊙O相交,此时d与r大小关系为_________ldrd=rd0)2.利用直线与圆的公共点的个数进行判断：2220()()设方程组消元所得一元二次方程的解的个数为AxByCxaybrn直线与圆相离直线与圆相切直线与圆相交n=0n=1n=2△<0△=0△>0例1.如图，已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0，判断直线l与圆的位置关系；如果相交，求它们交点的坐标..xyOCABl解法一：由直线l与圆的方程，得22360,240.xyxyy①②消去，得y2320xx因为2(3)42110,所以,直线l与圆相交，有两个公共点．解法二：圆为2222x+y-2y-4=0可化x+(y-1)=5,其圆心C的坐标为（0,1），半径长为5，点C（0,1）到直线l的距离223016551031d所以，直线l与圆相交，有两个公共点．由2320,xx解得122,1.xx把x1=2代入方程①，得y1=0；把x2=1代入方程①,得y2=3.所以，直线l与圆有两个交点，它们的坐标分别是A（2,0）,B（1,3）.•1.判断直线3x+4y+2=0与圆x2+y2-2x=0的位置关系为。•2.直线y=mx+4与圆x2+y2=4相切，则m=。•3.请判断引入新知中的问题情景中的直线与圆的位置关系。练习2的变式：判断直线mx-y+2=0与的位置关系。同学们，你们能用几种方法判断呢？变式1.若将例1改为求直线l：3x＋y－6＝0被圆C：x2＋y2－2y－4＝0截得的弦长．思路点拨：利用半径、半径和弦心距组成的直角三角形求解．我们可以有几种方法来求解呢？.xyOCABldr变式2已知过点M（-3，-3）的直线l被圆x2+y2+4y-21=0所截得的弦长为，求直线l的方程.45解：将圆的方程写成标准形式，得x2+(y+2)2=25,所以，圆心的坐标是（0，-2）,半径长r=5.如图，因为直线l被圆所截得的弦长是，所以弦心距为即圆心到所求直线l的距离为.4522455()525因为直线l过点M（-3，-3），所以可设所求直线l的方程为y+3=k(x+3),即kx-y+3k-3=0.根据点到直线的距离公式，得到圆心到直线l的距离因此，2233.1kdk22335.1kk即两边平方，并整理得到2k2-3k-2=0,解得k=，或k=2.所以，所求直线l有两条，它们的方程分别为y+3=(x+3),或y+3=2(x+3).即x+2y+9=0,或2x-y+3=0.23155,kk12121.直线Ax＋By＋C＝0与圆(x－a)2＋(y－b)2＝r2的位置关系及判断位置关系相交相切相离公共点个数__个__个__个几何法：设圆心到直线的距离d＝|Aa＋Bb＋C|A2＋B2d__rd__rd__r判定方法代数法：由Ax＋By＋C＝0，x－a2＋y－b2＝r2消元得到一元二次方程的判别式ΔΔ__0Δ__0Δ__0210＜＝＞＞＝＜2．直线与圆相交时弦长的求法．(1)几何法：如图，直线l与圆C交于A，B两点，设弦心距为d，圆半径为r，弦长为|AB|，则有|AB|22＋d2＝r2.即|AB|＝2r2－d2.乙(2)代数法：如图乙，①联立直线方程和圆的方程，解方程组得A，B点坐标，再由两点间的距离公式求弦长|AB|；②设直线l的方程为y＝kx＋b，联立直线l的方程与圆的方程，消去一个未知数得一个一元二次方程，利用根与系数的关系求解．2．求直线被圆截得的弦长的方法为：(1)应用圆中直角三角形：...