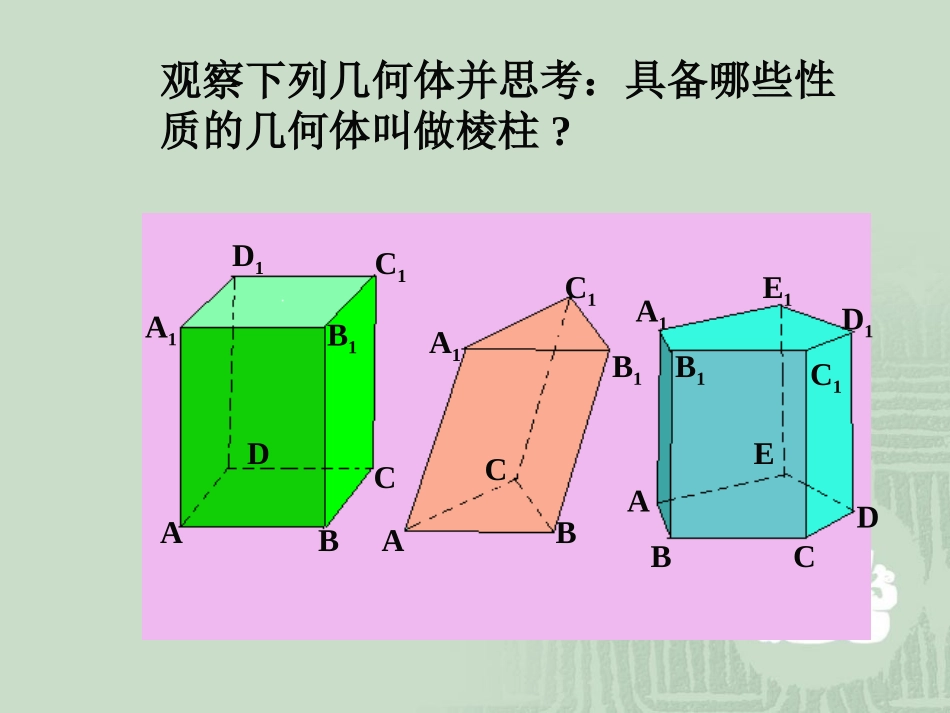
棱柱的概念和性质我们常见的一些物体,例如三棱镜,方砖以及螺杆的头部,它们都呈棱柱形状,如图:观察下列几何体并思考:具备哪些性质的几何体叫做棱柱?ABCDA1A1A1B1B1B1C1C1C1D1D1E1ABCABCDE棱柱与它的性质一、棱柱的概念:一个多面体有两个面,其余每相邻两个面的交线互相,这样的多面体叫做棱柱。互相平行互相平行观察下面的几何体,哪些是棱柱?问题问题11::有两个面互相平行,其余各面都是四边形的几何体是棱柱吗?答:不一定是.如右图所示,不是棱柱.问题问题22::有两个面互相平行,其余各面都是平行四边形的几何体是棱柱吗?答:不一定是.如右图所示,不是棱柱.棱柱的概念和性质棱柱的底面:棱柱的侧面:棱柱的侧棱:棱柱的顶点:两个互相平行的面除底面外的其余各面两个侧面的公共边侧面与底面的公共顶点顶点侧棱侧面底面棱柱的概念和性质棱柱的底面:棱柱的侧面:棱柱的侧棱:棱柱的顶点:棱柱的对角线:棱柱的高:两个互相平行的面除底面外的其余各面两个侧面的公共边侧面与底面的公共顶点不在同一个面上的两个顶点的连线两个底面的距离HH/对角线高1.用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE-A1B1C1D1E1二、棱柱的表示法2.用表示一条对角线端点的两个字母表示,如:棱柱AC1B1C1CA1BD1DABA1ACC1B1E1D1AEDBA1CC1B1三三..棱柱的分类棱柱的分类ABCDEA’B’C’D’E’(1)侧棱不垂直于底面的棱柱叫做斜棱柱按侧棱与底面是否垂直分(2)侧棱垂直于底面的棱柱叫直棱柱(3)底面是正多边形的直棱柱叫做正棱柱按底面多边形的边数分(1)三棱柱(2)四棱柱(3)五棱柱ABCDEA’B’C’D’E’棱柱的分类:根据底面边数分为:三棱柱、四棱柱、五棱柱等根据侧棱与底面是否垂直分为:直棱柱斜棱柱{按底面是否正多边形分为{正棱柱其它直棱柱这两种分类彼此又可渗透,例如斜三棱柱、直四棱柱、正五棱柱等正四棱柱正方体是哪一类棱柱?正四棱柱就是正方体,对吗?棱柱集合、斜棱柱集合、直棱柱集合、正棱柱集合之间存在怎样的包含关系?棱柱集合斜棱柱集合直棱柱集合正棱柱集合观察下列棱柱并思考:棱柱具备哪些性质?ABCDA1A1A1B1B1B1C1C1C1D1D1E1ABCABCDE四四..棱柱的性棱柱的性质质矩形平行四边形全等的矩形棱柱的性质1.棱柱的各个侧面都是,面都是;正棱柱的各个侧面都所有侧棱都相等;直棱柱的各个侧是已知:三棱柱ABC-A1B1C1求证:AA1=BB1=CC1,侧面ABB1A1是平行四边形ABCC1A1B1证明:底面ABC∥底面A1B1C1底面ABC∩平面ABB1A1=AB底面A1B1C1∩平面ABB1A1=A1B1}AB∥A1B1AA1∥B1B}侧面ABB1A1是平行四边形性质1侧棱都相等,侧面都是平行四边形。直棱柱的各个侧面都是矩形;正棱柱的各个侧面都是全等的矩形。的多边形;2.棱柱的两个底面与平行于底面的截面是对应边互相平行的棱柱的性质演示全等性质2两个底面与平行与底面的截面是全等的多边形ABCC1A1B1MNP已知:三棱柱ABC-A1B1C1,平面MNP∥底面ABC,且交三条侧棱于M、N、P求证:△MNPABC≌△平面MNP∥底面ABC平面MNP∩平面ABB1A1=MN平面ABC∩平面ABB1A1=AB证明:}MN∥ABAA1∥B1B}AMNBAB=MN……棱柱的性质平行四边形3.过棱柱不相邻的两条侧棱的截面是演示性质3过不相邻的两条侧棱的截面是平行四边形ABCA1B1C1D1D已知:四棱柱ABCD-A1B1C1D1求证:截面AA1C1C是平行四边形证明:四棱柱ABCD-A1B1C1D1AA1∥C1C=截面AA1C1C是平行四边形例1:下列命题中正确的()A、有两个面平行,其余各面都是四边形的几何体叫棱柱。B、有一个侧面是矩形的棱柱是直棱柱。C、有两个侧面是矩形的棱柱是直棱柱。D、有两个相邻侧面垂直与底面的棱柱是直棱柱。D练习:1、判断下列命题是否正确:①有一个侧面是矩形的棱柱是直棱柱。()③有两个相邻侧面是矩形的棱柱是直棱柱。()④一条侧棱垂直于底面两边的棱柱是直棱柱。()⑤侧面都是正方形的棱柱是正棱柱。()②有两个侧面是矩形的棱柱是直棱柱。()试验Á·Ï°1.gsp11、棱柱:、棱柱:①①侧棱都侧棱都,侧面和对角面都是,侧面和对角面都是;;②②两个底面与平行于底面的截面是两个底面与平行于底面的截面是。。22、直棱柱、直棱柱:①①各侧面和各对角面都是各侧面和各对角面都是;;②②...