高中数学 232平面的斜线和平面所成的角课件 新人教A版必修2 课件VIP免费

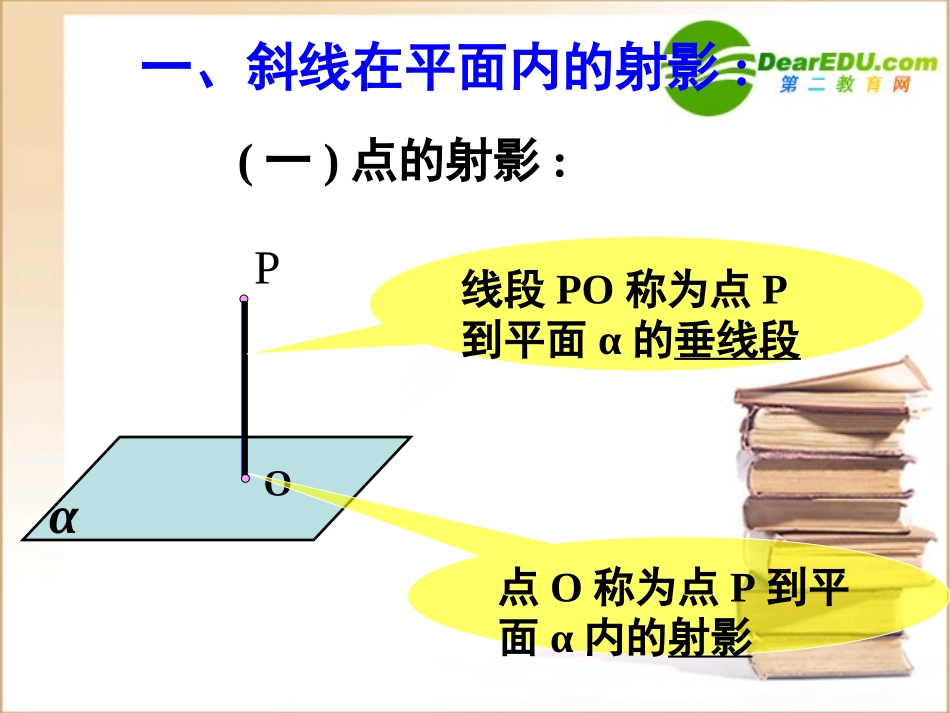
1、理解平面的斜线和平面所成的角的概念;2、掌握平面的斜线和平面所成的角的求法。一、斜线在平面内的射影:PO点O称为点P到平面α内的射影α线段PO称为点P到平面α的垂线段(一)点的射影:αOlO称为斜足直线l称为平面α的斜线线段PO称为点P到平面α的斜线段(二)斜线:PαOlP直线OQ称为斜线l在平面α内的射影线段OQ称为斜线段PO在平面α内的射影(三)斜线的射影:Q斜线上任意一点在平面上的射影，一定在斜线的射影上。思考:两条平行直线、相交直线、异面直线在同一个平面内的射影可能是哪些图形？平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角。简称线面角1、一条直线垂直与平面，它们所成的角是直角；2、一条直线和平面平行，或在平面内，它们所成的角是0的角。规定：二、平面的斜线和平面所成的角：1、直线与平面所成的角θ的取值范围是：2、斜线与平面所成的角θ的取值范围是：3、两异面直线所成的角θ的取值范围是：思考题：AGFEDCBHHC与平面ABCD所成的角是？BG和EA与平面ABCD所成的角分别是？∠GBC与∠EAB∠HCDEC和EG与平面ABCD所成的角分别是？∠ACE练习:正方体ABCD－EFGH中例1:在正方体ABCD-A1B1C1D1中，求直线A1B和平面A1B1CD所成的角.AC1DCB1OB1A1D10111013030所成的角为与平面即CDBABAOBAOAO，BCCB111,连结交于解：连结111111BCCBBO，BCCBBA面面BOBA11CBBO1所成的角与平面是上的射影在平面为面CDBABAOBA，CDBABAOA，DCBABO1111111111:22211知由中在BO，BA，BOARt线面角的计算小结:1、找出或作出线面角;2、证明（1）中的角就是所求的角;3、求出此角的大小。一“作”二“证”三“求”步骤:关键：确定斜线在平面内的射影.变式:在正方体ABCD-A1B1C1D1中，E，F分别是BC，CC1的中点，求EF与面ACC1A1所成的角.AC1DCA1D1BF1B1EOAOPCB特例：四面体P-ABC的顶点P在平面上的射影O(1)P到三顶点距离相等0是ABC的外心(3)P到三边AB、BC、AC距离相等0是ABC的内心(2)对棱相互垂直0是ABC的垂心PA、PB、PC两两垂直.2;1.30,,,:20所成的角与求所成的角与平面求的中点为，所成的角为与平面面例BEADABCADACEBCDADBCABCDBCBCDABAECBD【总一总★成竹在胸】1．直线与平面垂直的概念3．数学思想方法：转化的思想空间问题平面问题2．直线与平面垂直的判定、性质线线垂直线面垂直