辽宁省沈阳市二十一中高一数学(函数图象变换)课件VIP免费

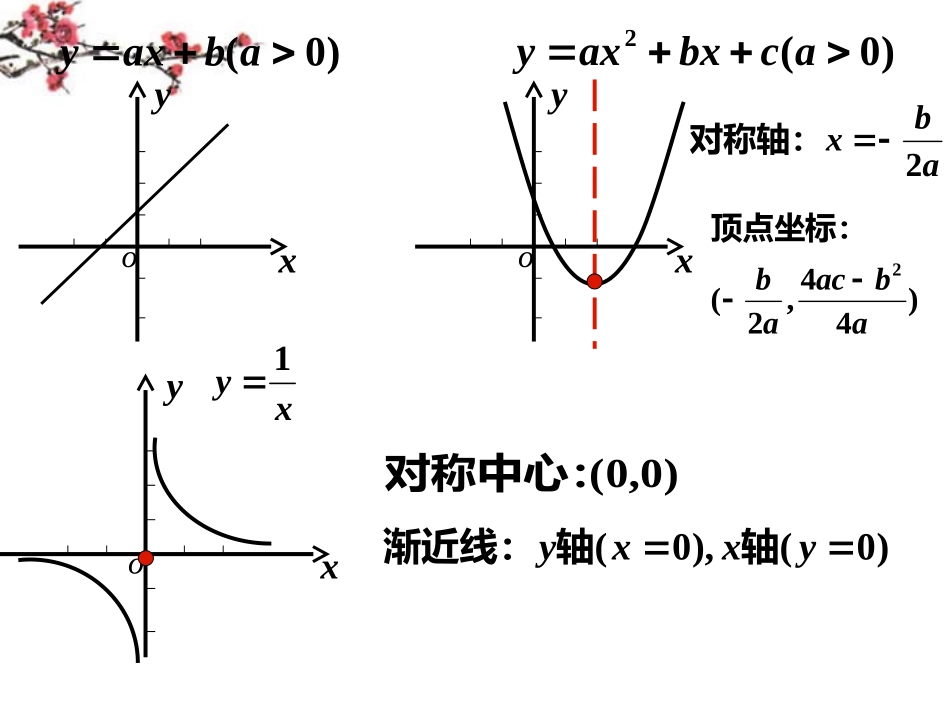
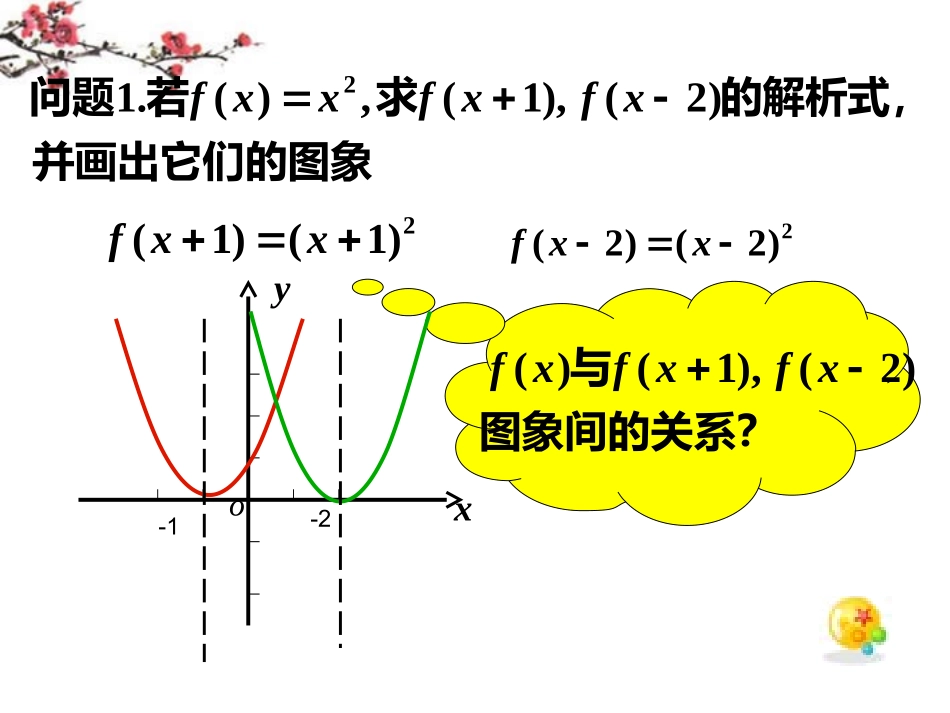
函数图象的平移变换•120中学数学组函数图象平移yxo)0(abaxyyxoabx2对称轴：)44,2(2abacab顶点坐标：)0(2acbxaxyyxoxy1)0(),0(yxxy轴轴渐近线：)0,0(对称中心：并画出它们的图象的解析式，求若问题)2(),1(,)(.12xfxfxxf2)1()1(xxf2)2()2(xxf图象间的关系？与)2(),1()(xfxfxfyxo-1-2并画出它们的图象的解析式求若问题2)(,21)(,)(.22xfyxfyxxf2121)(2xxf22)(2xxfyxo-221图象间有什么关系？与2)(,21)()(xfxfxf平移变换)(xfy个单位向左平移a)(axfy0a)(xfy个单位向右平移a)(axfy0a)(xfybxfy)(个单位向上平移b0b)(xfybxfy)(个单位向下平移b0b个单位向右平移a个单位向左平移a个单位向下平移b个单位向上平移b个单位得到的再向左平移个单位，向下平移是由322)3()(.4xfyxfy3131.1xyxy个单位得到向右平移错误，请改正（一）判断正误，如果练习1313.2xyxy个单位得到向左平移个单位得到的向右平移是由55.3xyxyyxo-11yxo-2yxo-11(A)(B)(D)31yxo223yxo12(C)的图象大致为的图象如右，则已知函数（二）选择：)2()(.1xfyxfyyxo-11yxo-2yxo-11(A)(B)(D)31yxo223yxo12(C)的图象大致为的图象如右，则已知函数选择：2)()(.2xfyxfy的图象大致为的图象如右，则已知函数选择：2)2()(.3xfyxfyyxo-11yxo-2yxo-11(A)(B)(D)31yxo223yxo12(C)_________3_________,21.1个单位，得到再向上平移个单位，得到向左平移将（三）填空：xy_____________2________,31.2个单位，得到再向左平移个单位，得到向上平移将xy21xy321xy31xy321xy如何平移得到的？是由思考：xyxxy1273__________________2)2(.3单位得到向左平移xf的图象画出的解析式写出思考：)]2(2[),22(),2(,)]2(2[),22(),2(,)(2xfxfxfxfxfxfxxf)22(xfxo24)2(xxf22)1(4)22()22(xxxf2)2(4)]2(2[xxf)]2(2[xf2)22()22(xxf24)2(xxf2)2(4)]2(2[xxf身上体现。平移的量值要在而言，动是针对注意：横向平移xx_________1)2(.4单位，得到个向右平移将xfy_________2)3(.5得到个单位，向右平移xfy)]1(2[xfy)]2(3[xfy_____________)()0,0)((.6axfybabaxfy是将个单位向左平移ab_____________1)(.7得到个单位，向左平移xf)]1([xfy______________23)2(.8个单位向右平移xf)]23(2[xfy的图象利用平移画出应用21.1xyxy1212xy个单位向左平移对称中心如何移动？个单位图象上所有点向左移动作图关键：2.1渐近线如何移动？.2？图象的大体形状改变么.3yxo的原始形状保持图形在新的范围内画图要移动有渐近线的，渐近线也移动找准特殊点，观察它的步骤：,.3.2.1的图象作出应用273.2xxy如何平移得到的？是由平移过程，思考：xyxxy1273.1成哪个点？对称中心如何移动？变.2渐近线如何移动？.3yxo_____________________________)2(1)12(.9经过怎样的变换得到的是由xfxfy1)2()2(1xfyxfy个单位向下平移)12()2(21xfyxfy个单位向左平移个单位向下平移11)12(xfy个单位向左平移21