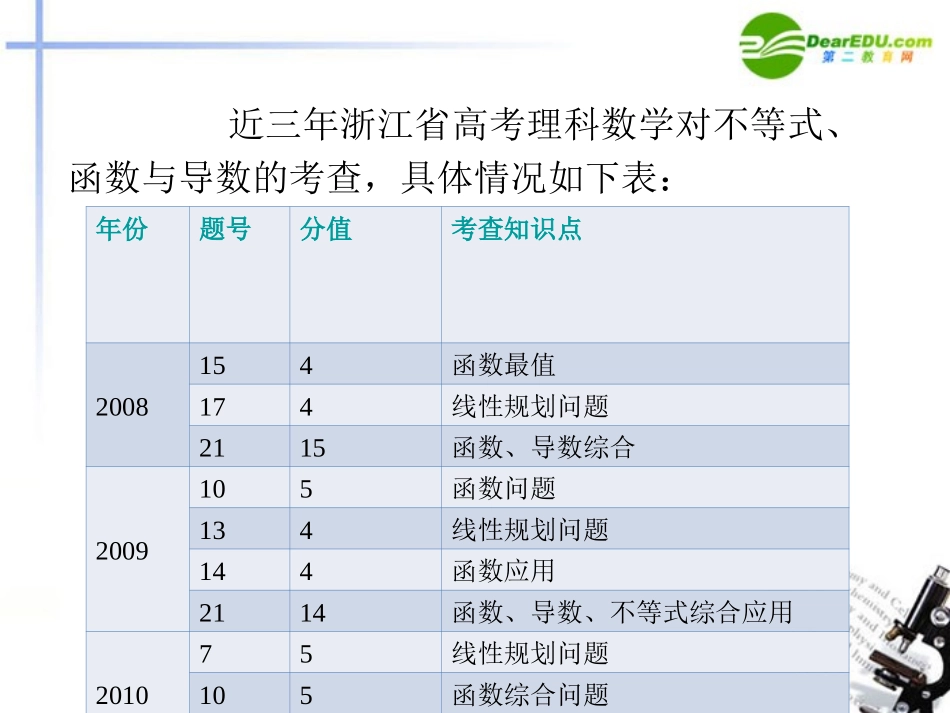
专题一不等式、函数与导数年份题号分值考查知识点2008154函数最值174线性规划问题2115函数、导数综合2009105函数问题134线性规划问题144函数应用2114函数、导数、不等式综合应用201075线性规划问题105函数综合问题2214函数、导数和等差数列近三年浙江省高考理科数学对不等式、函数与导数的考查,具体情况如下表:从上表中可以看出,本专题是高中数学的核心内容之一,它的基本特点是数形兼备,在高考试题中占有举足轻重的地位,约占总分值的20%.其主要命题热点为:函数图象及其性质;基本不等式及其应用,线性规划问题;函数与导数的综合应用等.复习时应当注重函数的定义理解,函数的奇偶性、单调性的掌握,熟练掌握函数解析式的求法;熟练掌握一次、二次函数,幂、指数、对数函数等基本函数的图象与性质,掌握基本初等函数的导数公式及导数的四则运算,准确理解导数的几何意义及导数与函数性质的关系,学会解决函数与导数的综合应用问题.题型、题量、难度保持相对稳定,客观题主要考查函数的图象,线性规划问题,推理证明,基本不等式的应用等,解答题则是以函数为主要内容的综合题,问题涉及导数、不等式、数列等多方面知识,且难度较大,题型灵活.12()()1log()log()()0fxgxafxgxaafx不等式性质的使用条件,以及不等式是等价还是推出,这是不等式求解、证明、应用的基础.理解不等式解法的步骤及其原理,一次、二次,绝对值不等式,都用公式法解;分式不等式,高次不等式都用穿根法解.而指数、对数不等式是在保证表达式有意义的情况下,用函数的单调性转化求解..当时,;.当()()01log()log().()0fxgxafxgxaagx时,2(1)()0""1(2)2(22211134)xxaaxaaaaa含参数的不等式求解,在掌握好中方法的前提下,对参数的讨论是非常自然的,甚至它不应该成为一个难点.如解要用穿根法,标根时与,的位置关系不定,自然分五类即,,,和,分别穿根写解集即可.注意体会函数、方程、不等式问题的广泛联系及..灵活转化.【例1】比较1+logx3与2logx2(x>0且x≠1)的大小.差值比较法.3(1log3)-2log2log.4011301334011443log01log32log()24xxxxxxxxxxxxxx当或,即<<或>时,有>以>ⅰ,所;011331014434log0.143431(log0,1log32log2343431log04341log32lo)(2.)gxxxxxxxxxxxxxxxxxx当①或②时,<解①得无解,解②得<<,即当<<时,有<<;当,即时,ⅲ有,所以ⅱ4011log32log23411log32log2341log32log2.3xxxxxxxxxx综上所述,当<<或>时,;当<<时,;当时,,1.logax的符号规律要记准,这是本题分类讨论的根源.2.对变量讨论时最好转化为不等式组的形式,否则容易忘掉与大前提求交集.3.对变量讨论与对参数讨论在结果的表述上有区别.1211--1.211--1.11-2-1.xyzxyzyzxyzxxxxxyzxyzzzzyxzxzyyyy因为,,是互不相等的正数,且,所以①②③1111(1)(1)(1)8.xyzxyzxyz已知,,是互不【变式训练】相等的正数,且,求证:111011111(-1)(.1-1)(-1)8.1.xxzyxyz又因为,所以同理,将①②③三式相乘得【例2】已知实数a≠0,函数f(x)=ax(x-2)2(x∈R).(1)若函数f(x)有极大值,求实数a的值;(2)若对∀x[-2,1]∈,不等式f(x)<32恒成立,求实数a的取值范围.3227极值问题可利用导数解决,恒成立问题可转化为最值问题或参变分离.322()-44()3-84(3-2)(-2)2()02.1.332()2723220()3271fxaxaxaxfxaxaxaaxxfxfxffax,.令,得或因为有极大值,而,所以,解得maxmax()(3-2)(-2)220()[-2][1]332()()3227027.3220()[-2][1-1,0]33-2-321()-3232-01,27210..-fxaxxafxfxfaaaafxfafafxaaaa,当时,在,上递增,在,上递减,,即,所以当时,在,上递减,在,上递增,,所以,即,所上以综可得恒成立问题通过变形后,一般都化为最值问题来处理.【变式训练】(1)若对任意x>0,≤a...