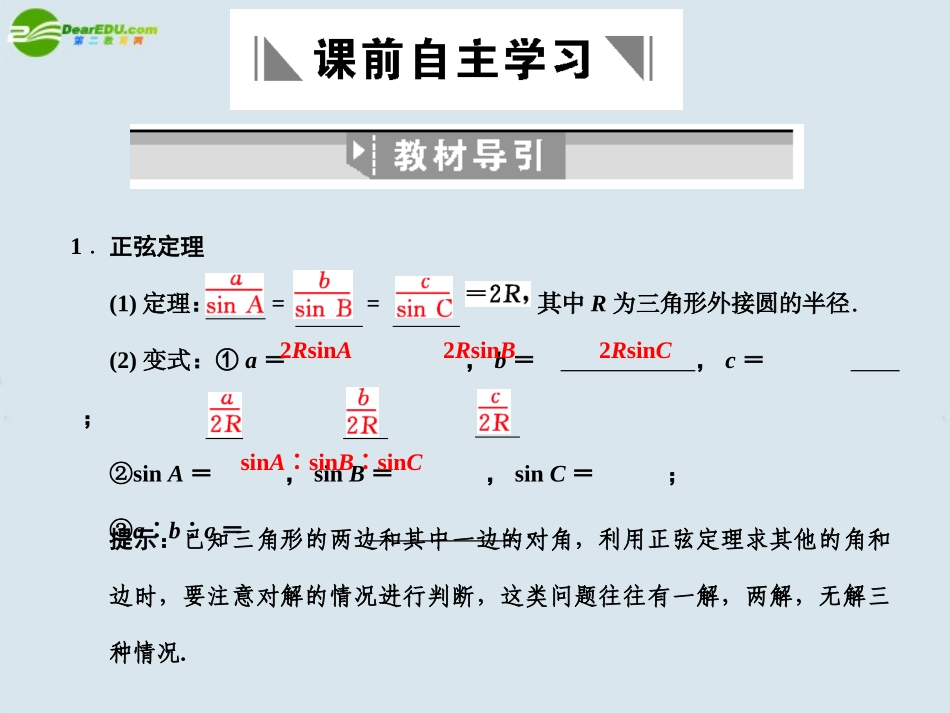
【考纲下载】1.掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.2.能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.第7讲正、余弦定理及其实际应用正弦定理(1)定理:==其中R为三角形外接圆的半径.(2)变式:①a=,b=,c=;②sinA=,sinB=,sinC=;③a∶b∶c=.2RsinA2RsinB2RsinCsinA∶sinB∶sinC1.提示:已知三角形的两边和其中一边的对角,利用正弦定理求其他的角和边时,要注意对解的情况进行判断,这类问题往往有一解,两解,无解三种情况.2.余弦定理(1)定理:a2=;b2=;c2=;(2)变式:cosA=;cosB=;cosC=.b2+c2-2bccosAa2+c2-2accosBa2+b2-2abcosC提示:在△ABC中,已知a,b,A,求c时,利用余弦定理a2=b2+c2-2bccosA得到关于c的二次方程,但也应注意三角形解的个数的判断.3.三角形面积公式(1)S=(ha表示a边上的高);(2)S=absinC==;(3)S=r(a+b+c)(r为内切圆半径).实际问题中的常用角(1)仰角和俯角与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线叫仰角;目标视线在水平视线叫俯角(如图①).上方下方4.(2)方位角指从方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②).正北(3)坡度:坡面与水平面所成的二面角的度数.提示:在解决与三角形有关的实际问题时,首先要明确题意,正确画出平面图形或空间图形,然后根据条件和图形特点将问题归结到三角形中解决.1.△ABC的内角A,B,C的对边分别为a,b,c.若c=,b=,B=120°,则a等于()解析:由正弦定理得又 C为锐角,则C=30°,∴A=30°,△ABC为等腰三角形,a=c=.答案:D2.(2009·广东卷)已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c.若a=c=+,且∠A=75°,则b=()解析: a=c,∠A=75°,∴∠B=30°,∴b2=a2+c2-2accos30°∴b=2.答案:A3.已知锐角△ABC的面积为3,BC=4,CA=3,则角C的大小为()A.75°B.60°C.45°D.30°答案:B4.在200m高的山顶上,测得山下一塔的塔顶和塔底的俯角分别是30°、60°,则塔高为________m.在△ACD中,由余弦定理得,解析:如图,由已知可得∠BAC=30°,∠CAD=30°,∴∠BCA=60°,∠ACD=30°,∠ADC=120°,判断三角形的形状,应围绕三角形的边角关系进行思考,主要看其是否是正三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.依据已知条件中的边角关系判断时,主要有如下两条途径:(1)利用正、余弦定理把已知条件转化为边边关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状;(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形,得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.在中,分别表示三个内角的对边,如果,判断三角形的形状.思维点拨:利用正弦定理、余弦定理进行边角互化,转化为边边关系或角角关系.【例1】解:解法一:已知等式可化为a2[sin(A-B)-sin(A+B)]=b2[-sin(A+B)-sin(A-B)]∴2a2cosAsinB=2b2cosBsinA由正弦定理可知上式可化为:sin2AcosAsinB=sin2BcosBsinA∴sinAsinB(sinAcosA-sinBcosB)=0∴sin2A=sin2B,由0<2A,2B<2π,得2A=2B或2A=π-2B,即A=B或A=-B,∴△ABC为等腰或直角三角形.解法二:同解法一可得2a2cosAsinB=2b2sinAcosB,由正、余弦定理,可得∴a2(b2+c2-a2)=b2(a2+c2-b2)即(a2-b2)(a2+b2-c2)=0∴a=b或a2+b2=c2,∴△ABC为等腰或直角三角形.三角形一般由三个条件确定,比如已知三边a,b,c,或两边a,b及夹角C,可以将a,b,c或a,b,C作为解三角形的基本要素,根据已知条件,通过正弦定理、余弦定理、面积公式等利用解方程组等手段进行求解,必要时可考虑作辅助线,将所给条件置于同一三角形中.(1)求△ABC的面积;(2)若c=1,求a的值.形面积公式求解即可;(2)根据第(1)问求出的bc,结合b+c就可以求出b,c的值,根据余弦定理求解.解:(1)因为得bccosA=3,所以bc=5.因此S△ABC=bcsinA=2.(2)由...