高中数学 直线与圆锥曲线的位置关系课件 新人教A版选修2-1 课件VIP免费

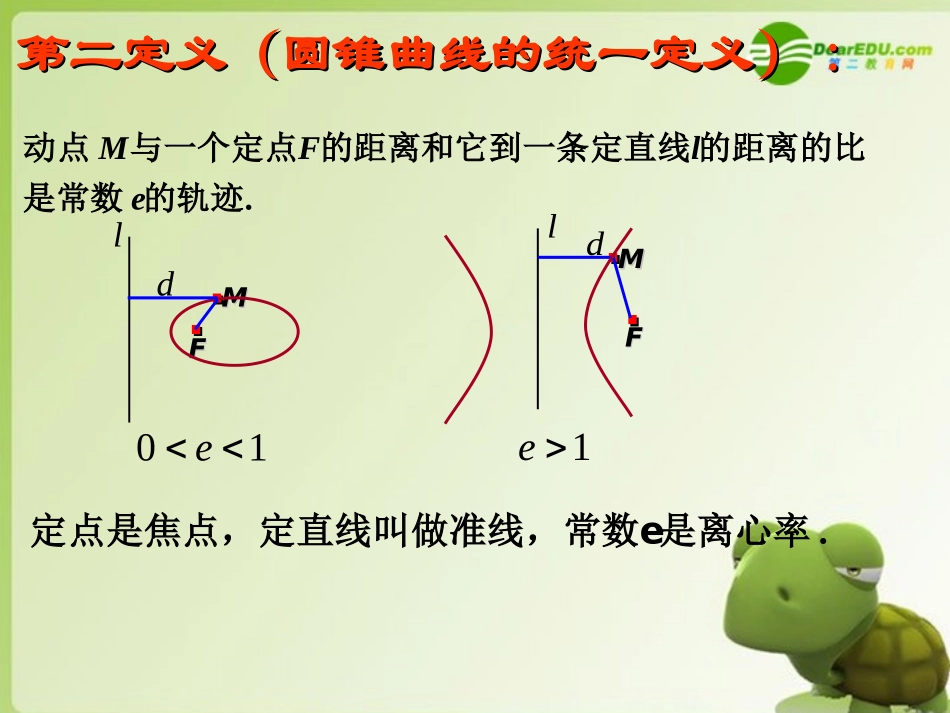
12222byax)0(ba12222byax)0,0(ba定义定义::12212121(1):,(|||||||2}.(2||)).,FFPPFPFaaFFFF椭圆平面内到两个定点的距离的和等于常数大于的点的轨迹叫做椭圆两个定点叫做两个焦点的距离叫做{焦点焦距.12212112(2):,(||).{|||||2}.(2||),PPFPFaaFFFFFF双曲线平面上到两个定点的距离的差的绝对值等于常数小于的点的轨迹叫做双曲线这两个定点叫做两焦点间的距离叫做焦点焦距.第二定义（圆锥曲线的统一定义）第二定义（圆锥曲线的统一定义）::.MFle动点与一个定点的距离和它到一条定直线的距离的比是常数的轨迹.定点是焦点，定直线叫做准线，常数e是离心率l..FFdMM..10el..FFdMM..1e12222byax)0(ba12222byax)0,0(ba椭圆椭圆双曲线双曲线几何条件几何条件与两个定点的距与两个定点的距离的和等于定值离的和等于定值与两个定点的距离的差的绝与两个定点的距离的差的绝对值等于定值对值等于定值标准方程标准方程图形图形顶点坐标顶点坐标yyxxBB11BB22AA11AA22OOyyxxooFF22FF11MM),0(),0,(ba)0,(a对称轴对称轴焦点坐标焦点坐标离心率离心率准线方程准线方程渐近线方程渐近线方程yxB1B2A1A2OyyxxooFF22FF11MMax2,长轴长轴by2,短轴长轴ax2,实轴长轴by2,虚轴长轴)0,(c22bac)0,(c22bacace10e1ecax2cax2xaby椭圆椭圆方程方程图形图形范围范围对称性对称性顶点顶点离心率离心率12222byax12222bxayYYXXBB22BB11AA22AA11ooFF11FF22bybaxa,ayabxb,关于关于xx轴，轴，yy轴，轴，原点原点,,对称。对称。关于关于xx轴，轴，yy轴，轴，原点原点,,对称。对称。),0(),0,(bBaA)0,(),,0(bBaA)10(eace)10(eacecax2准线方程2ayc准线方程xxyyBB22BB11AA11AA221F2F例1求椭圆16x2+25y2=400的长轴和短轴的长、离心率、焦点和顶点坐标把已知方程化成标准方程得2222154xy5,4,25163abc这里因此，椭圆的长轴长和短轴长分别是210,28ab离心率30.65cea焦点坐标分别是)0,3(),0,3(21FF四个顶点坐标是1212(5,0),(5,0),(0,4),(0,4)AABB解:222525,.xy求椭圆的长轴和短轴的长焦点和顶点的坐标练习练习::解解::5,1,25126.abc221,25yx椭圆的标准方程为(0,26),(0,5),(1,0).F焦点顶点210.22,ab长轴长短轴长P2Fx1FyO12,PFPF245.a由此得221.4520xy所求椭圆的方程为例21212,,,FFPFPFP为两焦点且若点到两准线的距离612,.分别为和求椭圆的标准方程,,xP已知椭圆的焦点在轴上为椭圆上一点解:2,c焦距为2222,1,xyab如图设椭圆方程为：12||||,,612PFcPFcaa由椭圆第二定义得22221212||||||(2),PFPFFFc22222361444cccaa22226122,5.20.acbacc又6122222650,6910.:,3,xyxxyx一动圆与圆外切同时与圆内切求动圆圆心的轨迹方程并说明它是什么样的曲线例分别将两已知圆的方程配方2234,xy得223100.xyxyNPMoR1o2o解法一解法一::12,,.OO半径为R两已知圆的圆心分别为,,,Pxy如图设动圆的圆心1,PO当圆与圆外切时有12,OPR①2,PO当圆与圆内切时有210.OPR②,两边分别相加得②①1212,OPOP2222:3312.xyxy即③222312.xyx④,:两边分别平方得将④22341080xy221.3627xy12,63,它的长轴和短轴长分别为如图中虚线所示,动圆圆心的轨迹是椭圆xyNPMoR1o2o:解法二同解法一得方程12,,3,03,012,126PxyOO由方程可知动圆圆心到点和的距离和为常数且P点的轨迹为椭圆:26,212ca即3,6ca236927.b221.3627xy,12,63.动圆圆心的轨迹是椭圆长轴和短轴长分别为1212,OPOP例例4:4:2212221(0),,,xyPabFFab设是椭圆上一点是焦点21212,:.PFPFFPFb若求证的面积是FF22FF11ooPPxxyy又又|F|F11FF22|=2c|=2c，，PFPF11PF⊥PF⊥22，，如图如图,,由椭圆的定义得由椭圆的定义得|PF|PF11|+|PF|+|PF22|=2a|=2a证明证明::由此得由此得|PF|PF11||22+|PF+|PF22||2...