高中数学 24等比数列课件4 新人教A版必修5 课件VIP免费

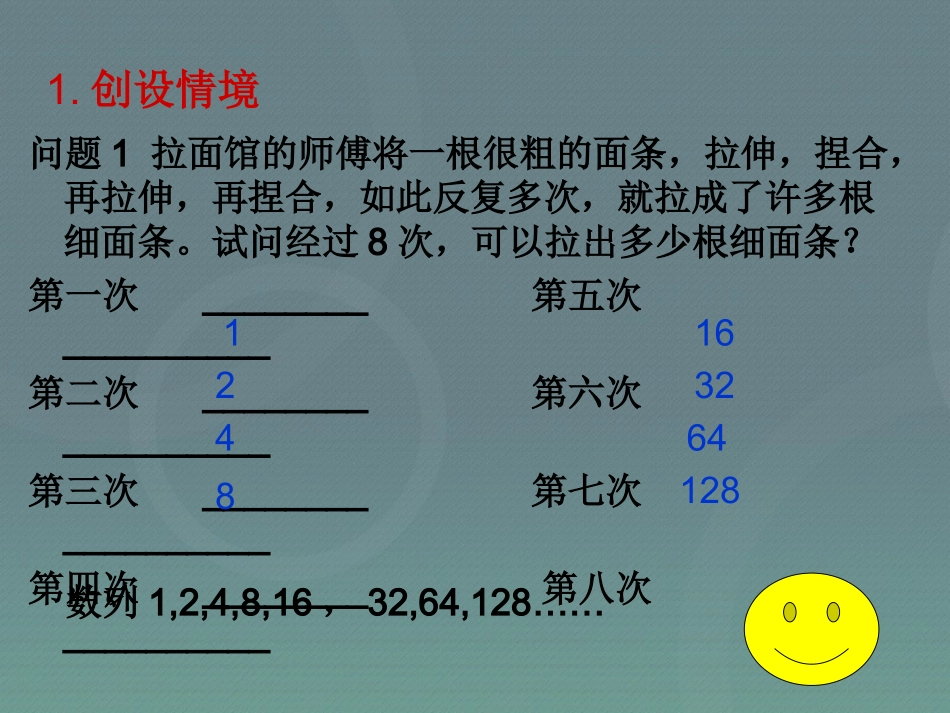
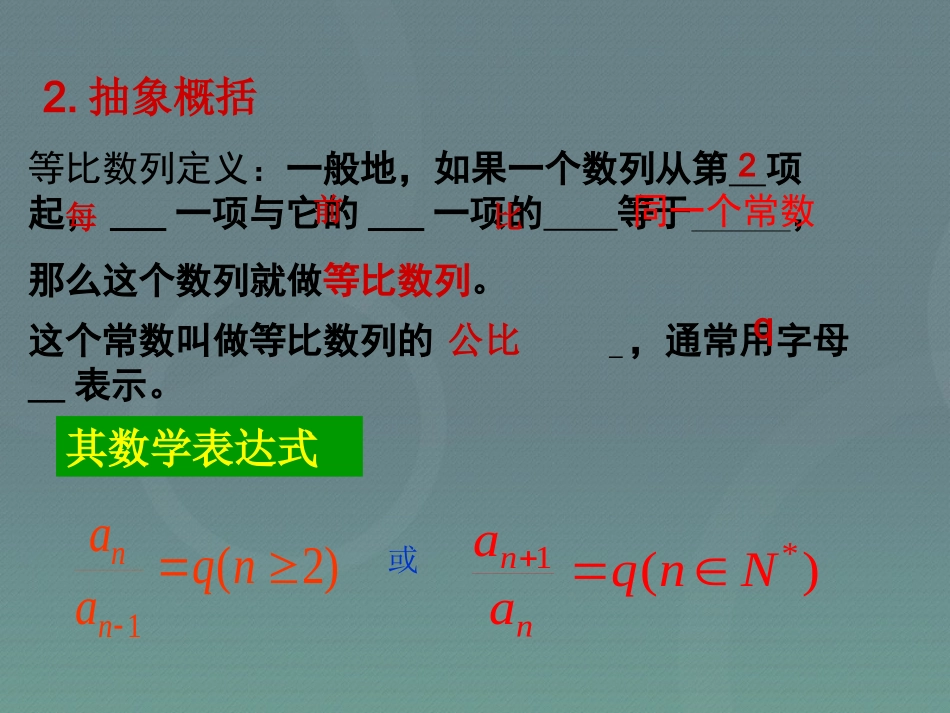
问题1拉面馆的师傅将一根很粗的面条，拉伸，捏合，再拉伸，再捏合，如此反复多次，就拉成了许多根细面条。试问经过8次，可以拉出多少根细面条？第一次________第五次__________第二次________第六次__________第三次________第七次__________第四次________第八次__________4218163264128数列1,2,4,8,16，32,64,128……1.创设情境)2(1nqaann或)(*1Nnqaann其数学表达式等比数列定义：一般地，如果一个数列从第项起，___一项与它的___一项的等于，那么这个数列就做等比数列。这个常数叫做等比数列的_，通常用字母__表示。比同一个常数2公比q2.抽象概括每前请同学们根据自己理解的定义写出一个等比数列。3.分析总结4.自主探究：（1）你能根据等比数列的定义推导出等比数列的通项公式吗？)2(1nqaann方法一qaa12qaa23qaann1qaa122123qaqaa……∵∴……3134qaqaaqaa34猜想：an=a1qn-1不完全归纳法方法二qaa12qaa23qaann1qaa122123qaqaa……∵∴3134qaqaaqaa34an=a1qn-11133221......nnnnnqaqaqaqaa迭代法方法三把这n－1个等式左右两边同时相乘11342312...nnnqaaaaaaaa11nnqaa即通项公式为：an=a1qn-1qaaqaaqaaqaann1342312,,,,当n=1时，上面的等式也成立累乘法（2）等比数列的通项公式的结构特征是什么？5.技能提炼在等比数列{an}中：1,,,11naaqaqannn对于通项公式来说，有四个量，可以知三求一,162,3,21naqa,31,919qa1a（1）已知（3）已知求求n此题解法是利用数学的函数与方程思想，函数与方程思想是数学几个重要思想方法应熟悉并掌握。,27,1253aa21aa（3）已知求1221qa5741qa492q∴23q或23q23q时，当340,8,3162121aaaa23q当时，38,8,3162121aaaa等比数列的定义及通项公式的推导和应用函数与方程的思想类比知识内容研究方法思想方法课堂小结一题多解的思想思考：给你一张足够大的纸，假设其厚度为0.1毫米，那么当你把这张纸对折了42次的时候，所达到的厚度有多少？2的42次方大约为44亿千米地球到月球的距离为3.84亿米