高中数学 解斜三角形应用举例(一)课件 新人教A版必修5 课件VIP免费

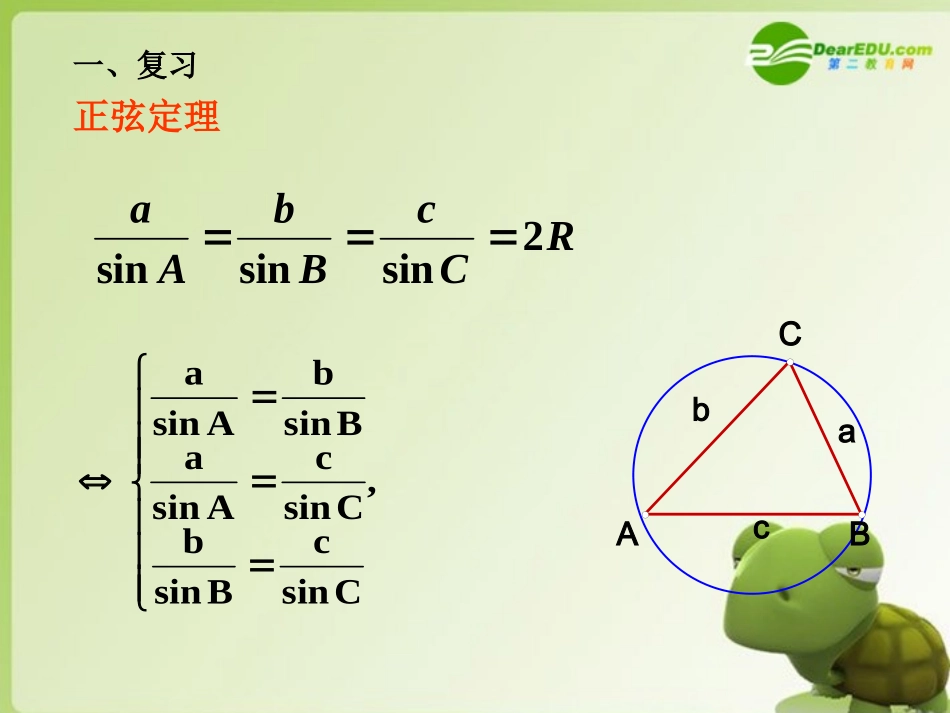
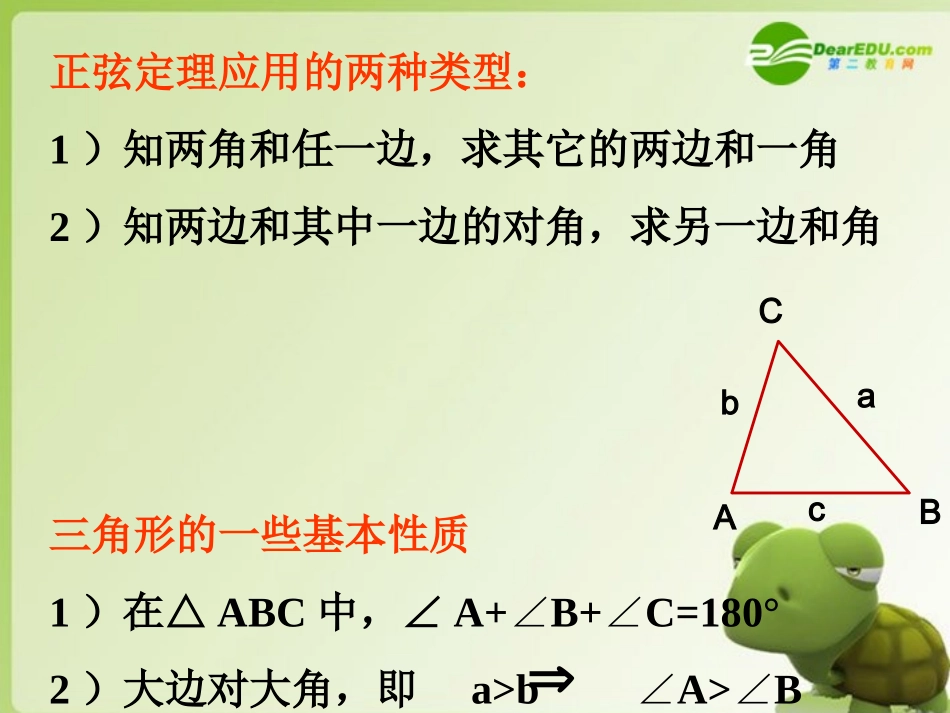
解斜三角形应用举例（一）一、复习正弦定理RCcBbAa2sinsinsin,CsincBsinbCsincAsinaBsinbAsinaABCabc正弦定理应用的两种类型：1）知两角和任一边，求其它的两边和一角2）知两边和其中一边的对角，求另一边和角三角形的一些基本性质1）在△ABC中，∠A+B+C=180°∠∠2）大边对大角，即a>bA>B∠∠ABCabc二、余弦定理Ccosab2bacBcosac2cabAcosbc2cba222222222ab2cbaCcosac2bcaBcosbc2acbAcos222222222ABCabc利用余弦定理可解决一下两类解三角形问题（1）知三边求三角（2）知两边和它们的夹角，求第三边，进而可求其它的角练习1、如图1，已知在Rt中，则BC=，AC=ABCACB,10,300ABBAC103002、如图2，已知在中，图1ABC,10,300ABBAC35ABC30010AC300，点B到边AC的距离是ABC外接圆的面积是图23310531005ABC则在ABC中，根据下列条件判断三角形的形状。（1）已知acosB=bcosA（2）已知cosA:cosB=b:a（3）已知三边长为：x2+x+1,x2-1,2x+1（4）已知lgsinB+lgsinC=2lgcos(A/2)三角形的形状判断三角形的形状判断几个概念：•仰角：目标视线在水平线上方的叫仰角;•俯角：目标视线在水平线下方的叫俯角；•方位角：北方向线顺时针方向到目标方向线的夹角。N方位角60度水平线目标方向线视线视线仰角俯角ABC因为某种实际需要，需测量左图中A、B二点间的距离。如何测量？800实际测量中，测量人员在如图所示位置取点C，用皮尺测得AC=8米，BC=5米，∠ACB=。由此测量人员可以得到AB的长度。问：怎么样算AB的长度？实际问题实际问题数学化:在△ABC中，已知边AC，BC及∠C,求AB.800ABc58分析转化例1、上海的金茂大厦是世界上超高的标志性筑，有一位测量爱好者在与金茂大厦底部同一水平线上的B处测得金茂大厦顶部A的仰角15.66º，再向金茂大厦前进500米到C处后，测得金茂大厦顶部A的仰角为22.81º，他能否算出金茂大厦的高度呢？hA22.81º15.66º500mDBC解：∠ABD=17°,BD==29.8,ADsin14°sin17°BC=BDsin31°=15.3,DC=BDcos31°=25.5.答：树高15.3m,河宽25.5m.ADCB31014036cm求树高BC和河宽CD.例2ABCD30°45°30°60°分析：1.在△ABD中求AB2.在△ABC中求AB46AB练习ABCD30°45°30°60°46AB23解：在中，ABC060ACDADCACD是等边三角形，则AD=CD=，2343345sin105sin23sinsin00DBCBCDCDBD00004510530180DBC8330cos433232)433()23(cos2022222ADBDBDADBDAAB练习1.自动卸货汽车的车厢采用液压机构.设计时需要计算油泵顶杠BC的长度.已知车厢的最大仰角为60°，油泵顶点B与车厢支点A之间的距离为1.95m，AB与水平线之间的夹角为6°20′，AC长为1.4m，计算BC长.BCA60°6°20′60°A1.95m6°20′1.40mBCBC60°A1.95m6°20′1.40m关键：应用余弦定理步骤：1.审题（明确已知、未知及术语）2.画图3.归结（在一个或几个三角形内）解：由余弦定理得)(89.1571.30266cos40.195.1240.195.1cos2022222mBCAACABACABBC答：顶杆BC约长1.89m//).AnmileCnmilehnmilehmin例3某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在处获悉,测出该渔船在方位角为45,距离为10的处,并测得渔船正沿方位角105的方向,以9的速度向小岛靠拢,我海军舰艇立即以21的速度前去营救,求舰艇的航向和靠近渔船所用的时间(精确到0.1,时间精确到1ABC10545北北:()21,9,45(180105)120.xhBABxBCxACB解设舰艇收到信号后在处靠垅渔船,则22222222cos(21)10(9)2109cos120.369100,2()40(min)().3ABACBCACBCACBxxxxxxh由余弦定理，得即化简,得解得负值舍去sin9sin12033,sin,211421.8,4521.866.8.BCACBxBACABxBAC由正弦定理得方位角为66.8,40min.答：舰艇应沿着方位角的方向航行经过就可靠近渔轮21x109x120方程的思想.,40,31,21,?CAACBCADCDA练习某观察站在城的南偏西20的方向,由城出发的一条公路走向是南偏东在处测得公路上处有一人距为千米正沿公...