高中数学 1.2.2空间两条直线的位置关系(2)课件 苏教版必修2 课件VIP免费

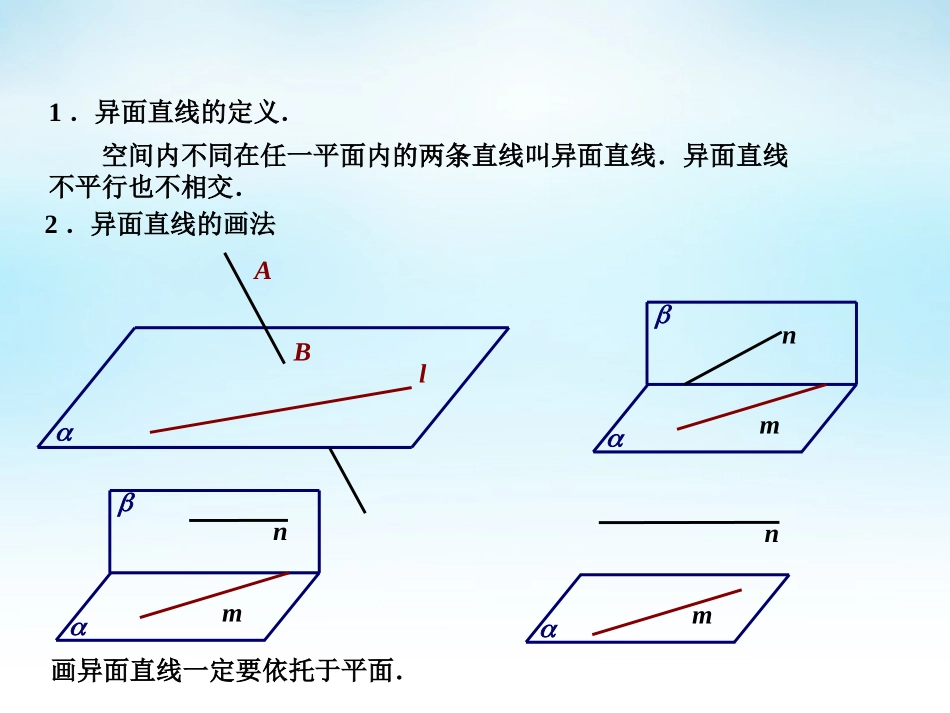
高中数学必修高中数学必修22高中数学必修高中数学必修221．空间两直线的位置关系．位置关系共面情况公共点个数相交在同一平面内有且只有一个平行没有异面不同在任一平面内复习回顾：2．平行公理．3．空间等角定理．对于异面直线，如何判定，又如何进一步刻画呢？1．异面直线的定义．空间内不同在任一平面内的两条直线叫异面直线．异面直线不平行也不相交．2．异面直线的画法ABlmnmnmn画异面直线一定要依托于平面．BB1AA1DD1CC1如图，长方体ABCD－A1B1C1D1的棱所在直线中，与直线AA1是异面的有________________________．如图，在长方体ABCD－A1B1C1D1中，相邻两个侧面的对角线A1B与异面CD，BC，B1C1，C1D1B1C的位置关系是____________．用反证法证明：空间四边形ABCD的对角线AC，BD是异面直线．DABC在空间四边形中，各边所在直线异面的共有几对？练习：例1．求证过平面外一点和平面内一点的直线，与平面内不经过该点的直线是异面直线．已知：A，B，Bl，l．求证：直线AB和l是异面直线．ABl定理：过平面外一点和平面内一点的直线，与平面内不经过该点的直线是异面直线．符号表示：若A，B，Bl，l，则直线AB与l是异面直线．——两点一线一面判定两条直线是异面直线的常用方法：反证法．练习：判断正误：①若a，b，则a，b为异面直线.②若a⊥b，b⊥c，则a∥c.③若a，b为异面直线，b，c为异面直线，则a，c也为异面直线.④若a，b共面，b，c共面，则a，c也共面.⑤一条直线和两条异面直线中的一条平行，则它和另一条直线不可能平行.小结：异面直线的判定：①利用定义；②判定定理：过平面外一点和平面内一点的直线，与平面内不经过该点的直线是异面直线．符号表示：若A，B，Bl，l，则直线AB与l是异面直线．——两点一线一面③常用方法：反证法．定量①空间内O点“任取”，说明角的大小与点O的位置选取无关，只由两直线的相对位置所确定；②a，b相交，转化为平面内两相交直线所成的角进行度量，立体问题平面化；③｛｜0º＜≤90º｝．——异面直线所成的角abOaba特别地：＝90º时，称两条异面直线互相垂直．记作：a⊥b．*空间两直线互相垂直，不一定有垂足．异面直线互相垂直一定没有垂足．AA1BB1CC1DD1例2．如图，在正方体ABCD－A1B1C1D1中，求下列各对异面直线所成的角O主要步骤：①构造平面角；②证明；③求角计算．转化为平面角(1)A1B与C1C；(2)AC与B1D1；(3)AC与BC1(4)A1B与B1D1．AA1BB1CC1DD1练习．如图，在正方体ABCD－A1B1C1D1中，E，F，M，N分别为所在棱的中点，求下列各对异面直线所成的角．OPEFMNL*中位线(1)EF与MN；(2)EF与BD1．例2．空间四边形ABCD中，E，F分别是对角线BD，AC的中点，(1)若BC＝AD＝2EF，求直线EF与AD所成角的大小．(2)若AB＝8，CD＝6，EF＝5，求AB与CD所成角的大小．BCDAEF练习：1.指出下列命题是否正确，并说明理由.①过直线外一点可作无数条直线与已知直线成异面直线.②过直线外一点只有一条直线与已知直线垂直.③若a∥b，c⊥a则b⊥c．④若c⊥a，b⊥c则a∥b．⑤分别与两条异面直线a，b都相交的两条直线c，d一定异面.2．如图，在正方体ABCD－A1B1C1D1中，与AD1所成角为60的面对角线有条AA1BB1CC1DD13.已知不共面的三直线a，b，c相交于点O，M，P是a上两点，N，Q分别在b，c上．求证：MN，PQ异面.acbOPMQN4.如图在三棱锥A-BCD中，E，F，G，H分别是边AB，BC，CD，DA的中点．①求证：四边形ABCD是平行四边形；②若AC＝BD，求证：四边形ABCD是菱形；③当AC与BD满足什么条件时，四边形ABCD是正方形?ABFCDHEG1．异面直线的判定．小结：①利用定义；②判定定理：若A，B，Bl，l，则直线AB与l是异面直线．——两点一线一面③常用方法：反证法．2．异面直线所成的角．作业：课本第30页练习4，5和第31页习题1．2（1）第10，11，14．