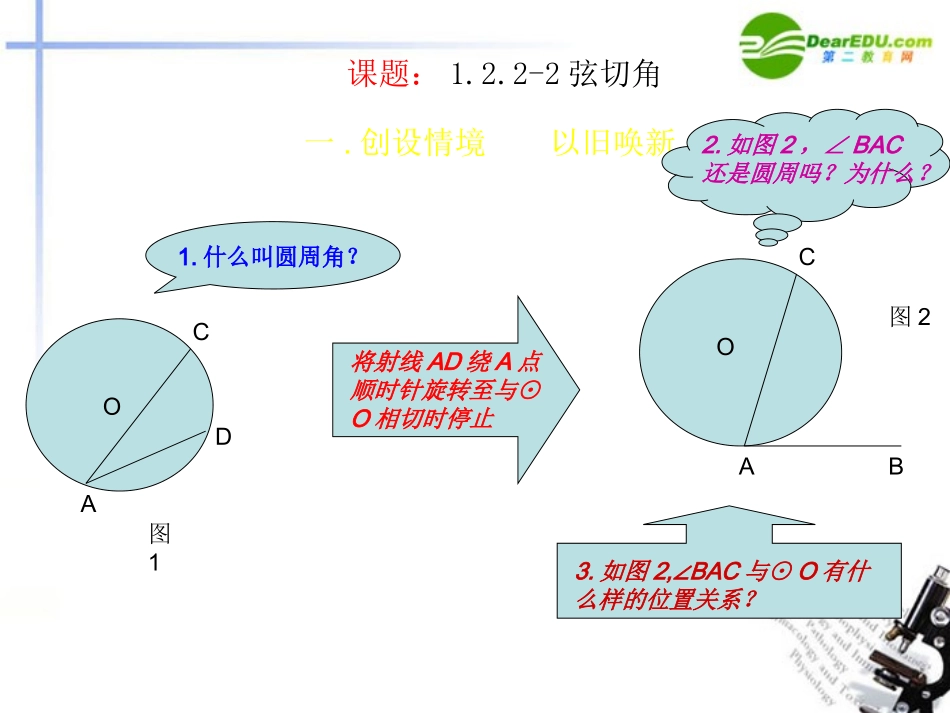
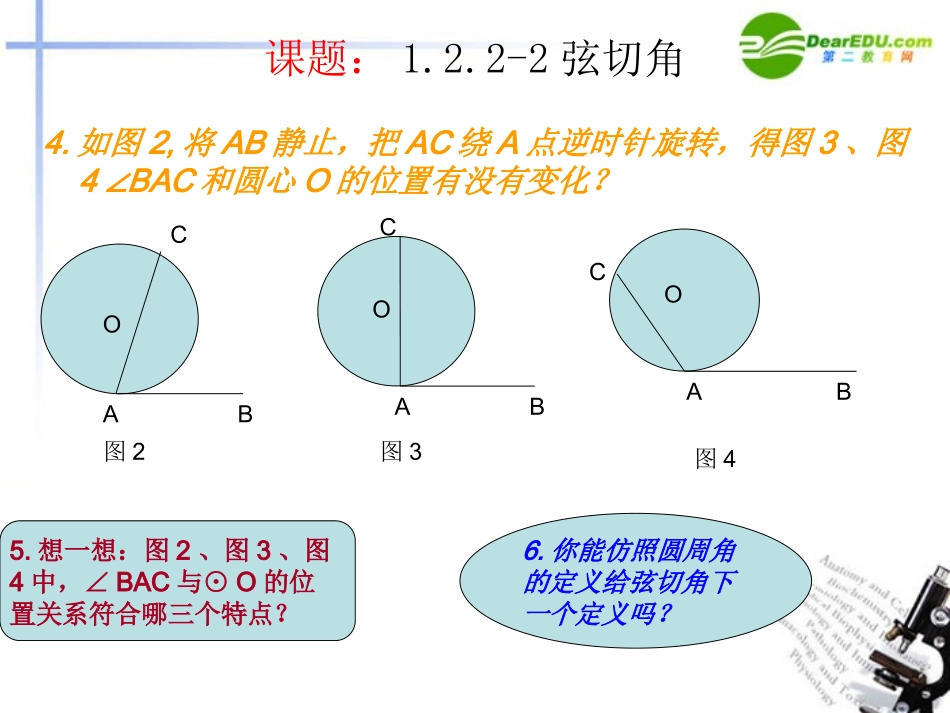
普通高中课程标准实验教科书(苏教版)几何证明选讲数学选修4-1课题:1.2圆的进一步认识1.2.2圆的切线2.弦切角p31-40东台市五烈镇中学杨荫林制作课题:1.2.2-2弦切角一.创设情境以旧唤新1.什么叫圆周角?ACD将射线AD绕A点顺时针旋转至与⊙O相切时停止OACB2.如图2,∠BAC还是圆周吗?为什么?3.如图2,BAC∠与⊙O有什么样的位置关系?O图1图2课题:1.2.2-2弦切角4.如图2,将AB静止,把AC绕A点逆时针旋转,得图3、图4BAC∠和圆心O的位置有没有变化?ABC图2图3图4ABCCOOOAB5.想一想:图2、图3、图4中,∠BAC与⊙O的位置关系符合哪三个特点?6.你能仿照圆周角的定义给弦切角下一个定义吗?课题:1.2.2-2弦切角二.寻找联系,发现规律APBCDEO7.图5,直线AB和⊙O相切于P,(1)图中哪些是弦切角,并指出它所夹的弧;(2)∠PBD、∠PDF是弦切角吗?为什么?图5FACDBP图68.图6中,找出与∠BAC相等的角,并说明依据9.在射线AB绕A点顺时针旋转的过程中,D点不断靠近A点,图7中∠BAC=∠P吗?为什么?继续旋转,图8中,会出现什么情形?ADBPC图7A、DPCB图810.想一想:图8中∠BAC还等于∠P吗?由此你有何猜想?课题:1.2.2-2弦切角猜想:弦切角的度数等于它所夹弧的度数的一半;或弦切角等于它所夹弧对的圆周角。ABC图9图10图11ABCCOOOAB1800Dn0n0D180011.圆周角定理的证明采用什么方法?弦切角的这一命题能否仿照证明吗?已知:求证:证明:分几种情况讨论三.类比联想,指导论证课题:1.2.2-2弦切角12.如图12,ABC⊿内接于⊙O,D是弧BC的中点,EF切⊙O于D,请指出图中与∠BDE相等的角。ABCDEF推论:同弧(或等弧)上的弦切角相等;同弧(或等弧)上的弦切角与圆周角相等。图12课题:1.2.2-2弦切角例4如图13,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,ADCE,⊥垂足为D,求证:AC平分∠BAD.证法一:证法二:ECDAB图13O想一想:有没有其它证明方法?课题:1.2.2-2弦切角四.巩固练习,指导应用例5(书p32)如图14,两圆内切于点P,大圆的弦AD与小圆相离,PA、PD交小圆于点E、F,直线EF交大圆于点B、C,求证:(1)EFAD∥(2)∠APB=CPD∠思路探索:PABCDMN图图1414如果两圆变成外切\相交等,结论如何?如果BC变成小圆的切线,结论又是怎样?(望同学们课后探讨)课题:1.2.2-2弦切角例6(书p32)如图15,AB、AC与⊙O分别切于点B、C,点P为⊙O上异于点B、C的任意一点,PDAB⊥于点D,PEAC⊥于点E,PFBC⊥于点F,求证:PF2=PD•PE思路探索:PDEBCFA想一想:本题中,如果点P在BC的劣弧上,如何画图,结论依然成立吗?图15课题:1.2.2-2弦切角五.归纳小结,整体把握(一)主要知识和内容1.弦切角的定义(理解,会识图):2.弦切角定理(了解证法,掌握定理):3.推论:4.定理和推论的应用5.数学思想方法:(二)……从弦切角的引入和定理的证明过程中,大家要逐步学会用运动变化的观点观察事物,逐步理解由此及彼,从一般到特殊,从特殊到一般的认识规律.自然科学都是如此.六.作业:A组课本p39第2、3、4题B组