高中数学：平面与平面垂直课件苏教版必修3 课件VIP免费

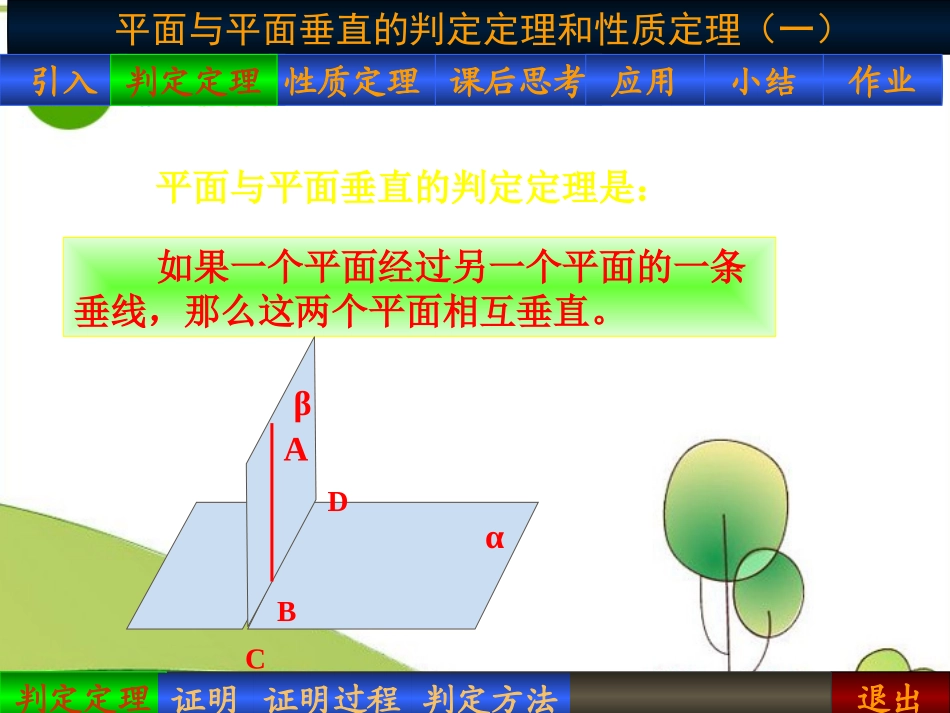
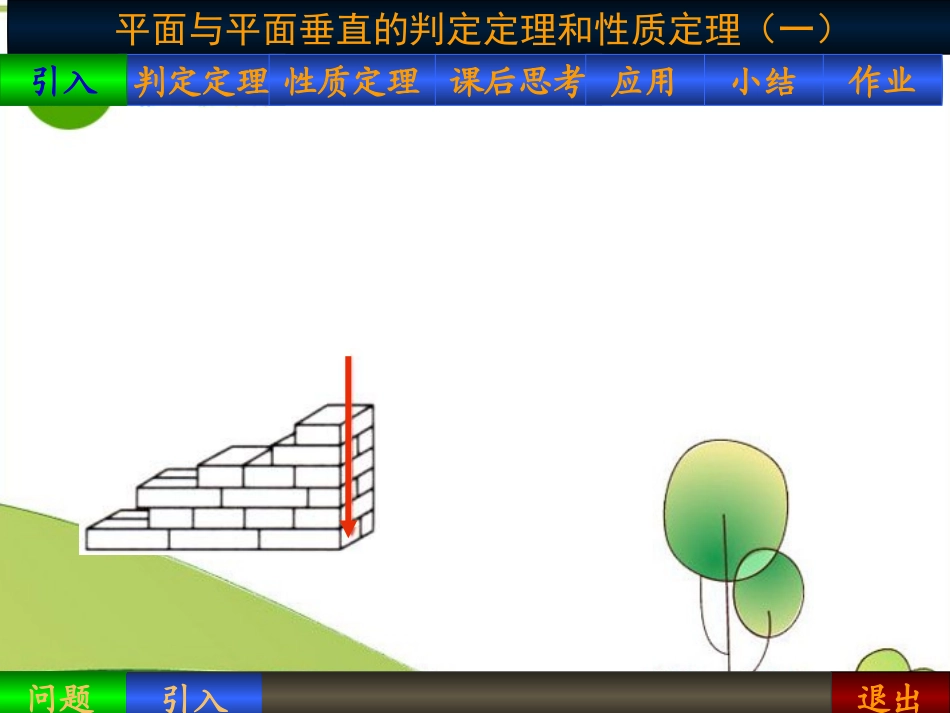
退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入问题2引入问题引入退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入判定定理证明过程判定定理平面与平面垂直的判定定理是：判定定理证明判定方法如果一个平面经过另一个平面的一条垂线，那么这两个平面相互垂直。βαABCD退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入建筑工人砌墙时，常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直，如果系有铅锤的线和墙面紧贴，问题引入引入那么所砌的墙面与地面垂直。大家知道其中的理论根据吗？退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入问题2引入引入问题——它就是本节课的内容之一：平面与平面垂直的判定定理。建筑工人砌墙时，常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直，如果系有铅锤的线和墙面紧贴，那么所砌的墙面与地面垂直。大家知道其中的理论根据吗？退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入判定方法判定方法证明判定定理证明过程判定定理找二面角的平面角说明该平面角是直角。（一般通过计算完成证明。）面面垂直的判定方法：1、定义法：2、判定定理：要证两个平面垂直，另一个平面的一条垂线。只要在其中一个平面内找到（线面垂直面面垂直）退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入应用1)例2解答例2题目例2题目例2、已知直线PA垂直于O所在的平面，A为垂足，AB为O的直径，C是圆周上异于A、B的一点。1)求证：平面PAC平面PBC；证明：2)例2解答AB是圆O的直径的一点C是圆周上异于A、BACBC平面ABCPA平面ABCBCPABC平面PAC平面PAC，PAACAPAAC平面PACBC平面PBCBC平面PBC。平面PAC退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入问题结论证明过程发现猜想注证明性质定理已知：平面⊥平面β，平面∩平面β=CD，求证：直线AB⊥平面β。AB⊥CD且AB∩CD=B。A平面，αβABCDE在平面β内过B点作BE⊥CD退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入问题证明结论证明过程发现猜想注结论性质定理如果两个平面相互垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。平面与平面垂直的性质定理是：αβABCD退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入练习2问题证明结论证明过程发现猜想注注性质定理1)面面垂直线面垂直；2)平面⊥平面β，要过平面内一点引平面β的垂线，只需过这一点在平面内作交线的垂线。（线是一个平面内垂直于两平面交线的一条直线）αβCDABαβCDAB退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入课后思考在刚才的三个条件中，。平面α直线AB平面β直线AB平面β平面α请判断命题的真假。若是真命题，请给出证明；若不是，那么添加什么条件可使命题为真？平面β。平面α平面α直线AB平面β直线AB再选取两个条件作为前提，另一个条件作为结论构造命题，即退出平面与平面垂直的判定定理和性质定理（一）判定定理性质定理课后思考应用作业小结引入小结2、“转化思想”线面关系线线关系面面关系线面平行线线平行线面垂直线线垂直面面垂直面面平行1、两个平面垂直的判定定理和性质定理3、平面⊥平面β，要过平面内一点引平面β的垂线，只需过这一点在平面内作交线的垂线。