高中数学 第一章第5节(三角函数的图象变换)课件 新人教A版必修4 课件VIP免费

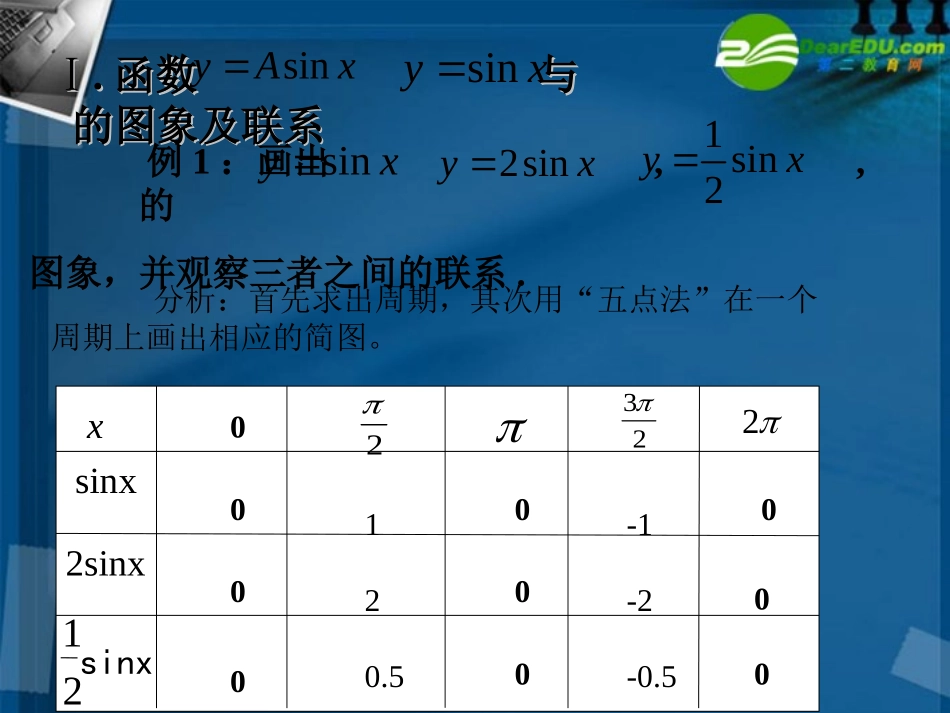
三角函数的图象换五点法作函数的简图])2,0[(sinxxy坐标依次为：（0，0）、（，1）、（，0）、（，-1）、（，0）2232.....xyo-2-234······-11复习:分析：首先求出周期，其次用“五点法”在一个周期上画出相应的简图。xsinx2sinxsinx000120.5000000-1-2-0.50212232ⅠⅠ..函数与函数与的图象及联系的图象及联系sinyAxsinyx例1：画出,,的图象，并观察三者之间的联系.2sinyxsinyx1sin2yx作图1sin2yxsinyx2sinyx223oxy212-1-2解：函数和的周期都为，我们先来作时函数的简图。列表：2sinyx1sin2yx2T[0,2]x对于同一个值,（或)的图象上点的纵坐标等于的图象上点的纵坐标的2(或1/2)倍x2sinyx1sin2yxsinyx2231-１2-2oxy3-32我们一起来观察它们之间的变化过程：2sinyx1sin2yxsinyx结论:图象上所有点的横坐标不变，纵坐标伸长到原来的2倍图象上所有点的横坐标不变，纵坐标缩短到原来的1/2倍sinyx2sinyxsinyx1sin2yx,的值域是:2sinyxxR[2,2],的值域是:1sin2yxxR11[,]22结论1:一般地,函数(且)的图像可以看作是把的图像上所有点的纵坐标伸长(当时)或缩短(当时）到原来的倍(横坐标不变)而得到.即sinyAx0A1Asinyx1A01AAsinyxsinyAx图象上所有点的横坐标不变,纵坐标伸长()或缩短()到原来的倍1A01AA的值域是:sinyAx[,]AA在相应区间上起关键点作用的五点，进而列表，画图。分析：用到“五点法”画图。在，上起关键作用的点为，这时我们就可令，则。sinyz[0,2]z3(0,0),(,1),(,0),(,1),(2,0)22xsinsinzsinyx就可对应求出又由的周期，我们来作的简图：1sin2yx4T[0,4]xsin2yx解：由函数的周期，我们来作的图象[0,]x22TⅡⅡ..函数与函数与的图象及联系的图象及联系sinyxsinyx例题2：画出画出,,,,的简图并观察它们之间的联系：的简图并观察它们之间的联系：sinyxsin2yx1sin2yxxx2x2sin424300102223100·····2-3223oxy211sinyxsin2yxxx21x21sin20340001022231·····1sin2yx223oxy2-324sinyx1-14xy21sin我们一起来观察它们之间的变化过程：？sinyxsin2yx223oxy22图象上所有点的纵坐标不变横坐标缩短到原来的½倍图象上所有点的纵坐标不变横坐标伸长到原来的2倍2232x1140sinyx1sin2yxsin2yxysinyxsin2yxsinyx1sin2yx结论2:图象上所有点的纵坐标不变，横坐标缩短()或伸长()到原来的1/ω倍101sinyxsinyx一般地,函数(ω>0且ω≠1)的图象,可以看作是把的图象上所有点的横坐标缩短(当ω>1时)或伸长(当0<ω<1时)到原来的1/ω倍(纵坐标不变)而得到的。即sinyxsinyx练习练习11：作下列函数在一个周期上的图象：（2）1sin3yx（1）;3sinyx第（1）题2xy03-33sinyxxy0第（2）题6π13π-11sin3yx我们今天学习了两个知识点:在以后大家就要学会用这种图象的变在以后大家就要学会用这种图象的变化解相应的知识化解相应的知识...Ⅰ函数与的图象及联系sinyAxsinyx.Ⅱ函数与的图象及联系sinyxsinyx作业:思考1、函数与的图象及联系及联系22、课本、课本)sin(xyxysin练习1（1），（2），（3），（4）73P