高中数学(正切函数的图像和性质)课件 新人教A版必修4 课件VIP免费

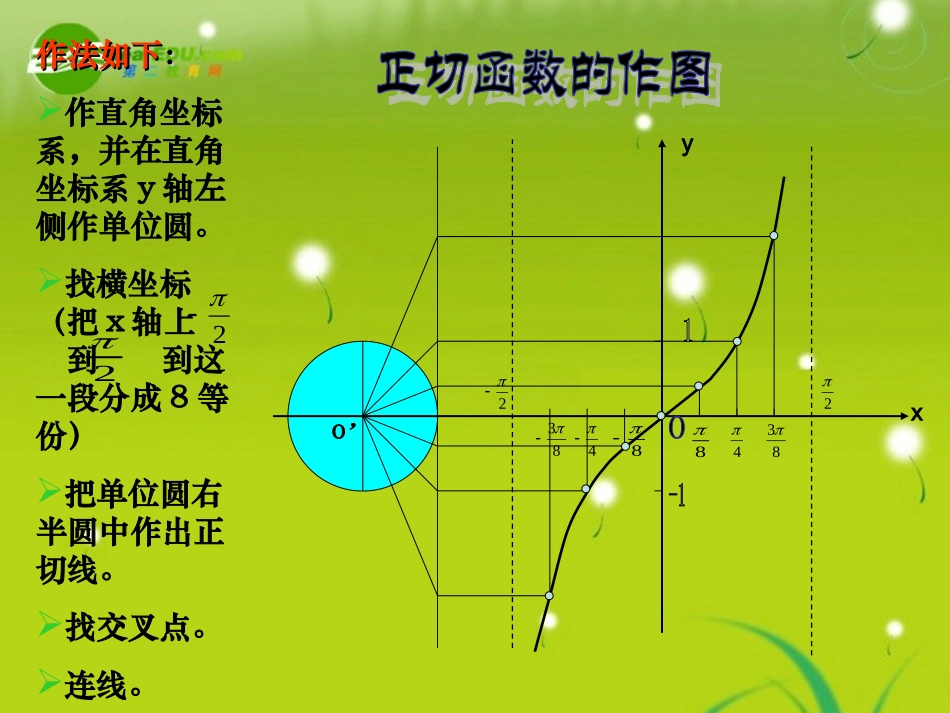
数学：《正切函数的图像和性质》课件ppt（新人教A版必修四）2作法如下作法如下：：作直角坐标系，并在直角坐标系y轴左侧作单位圆。找横坐标（把x轴上到到这一段分成8等份）把单位圆右半圆中作出正切线。找交叉点。连线。284838483xy22323全体实数RZkkxx,2|正切函数是周期函数，T=正切函数在开区间内都是增函数。Zkkk,2,2)tan()tan(xx正切函数是奇函数，正切曲线关于原点0对称)tan()tan(xx23223xyo例例11：：求函数的定义域。)4tan(xy解：解：令，那么函数的定义域是4xzzytan},2|{zkkzz由，得24kzx4kx所以原函数的定义域是：zkkxx,4|例2求函数的定义域、周期和单调区间.)32tan(xy,,232Zkkxx.,312Zkkx.,312|Zkkxx)32tan()32tan()(xxxf),2(3)2(2tanxfxZkkxk,2322.,231235Zkkxk.),231,235(Zkkk例题讲解例题讲解解:函数的自变量应满足即所以,函数的定义域是由于因此函数的周期为2.由解得因此,函数的单调递增区间是:解:函数的自变量应满足解:函数的自变量应满足巩固与提高巩固与提高1．观察正切曲线，写出满足下列条件的x的值的范围：（1）tanx＞0；（2）tanx=0；（3）tanx＜0．2．求函数y=tan3x的定义域．3．求下列函数的周期：)(24,2tanZkkxxy).()12(,2tan5Zkkxxy;143tan138tan与).517tan()413tan(与4．（1）正切函数在整个定义域内是增函数吗？为什么？（2）正切函数会不会在某一区间内是减函数？为什么？(1)(2)5．不通过求值，比较下列各组中两个正切函数值的大小：(1)(2)例3不通过求值，比较下列各组中两个正切函数值的大小：0167tan)1(;173tan0)411tan()2(与)513tan(与000018017316790)1(,tanxy在上是增函数00173tan167tan)43tan()411tan()2()53tan()513tan(,253432)2,2(,tanxxy)53tan()43tan()513tan()411tan(解解：：)270,90(00又且是增函数即又例4求下列函数的单调区间：);421tan(3)1(xy)42tan(3)2(xy变题uyxutan3,421)1(:则令解:421得由xu:)421tan(3的单调递增区间为xy24212kxk);42tan(3::xy因为原函数可化为解:u2x;tan4的单调性知由令yuZkkuk,22:421得由xu24212kxk:)421tan(3的单调递减区间为xy3(2,2),22kkkz:421;utan的单调性知由为增函数yxu22232kxk3(2,2),22kkkz23222kxk22kuk例5求下列函数的周期：);42tan(3)1(xy)42tan(3)(:xxf解);421tan(3)2(xy变题)42tan(3x]4)2(2tan[3x)2(xf2T周期)421tan(3)(:xxf解)421tan(3x]4)2(21tan[3x)2(xf2T周期||T周期（提示：利用正切函数的最小正周期来解）（1）正切函数的图像（2）正切函数的性质：定义域：值域：周期性：奇偶性：单调性：Zkkxx,2|全体实数R正切函数是周期函数，最小正周期T=奇函数，正切函数在开区间内都是增函数。Zkkk,2,2