高中数学 第2章本章优化总结课件 新人教A版必修5 课件VIP免费

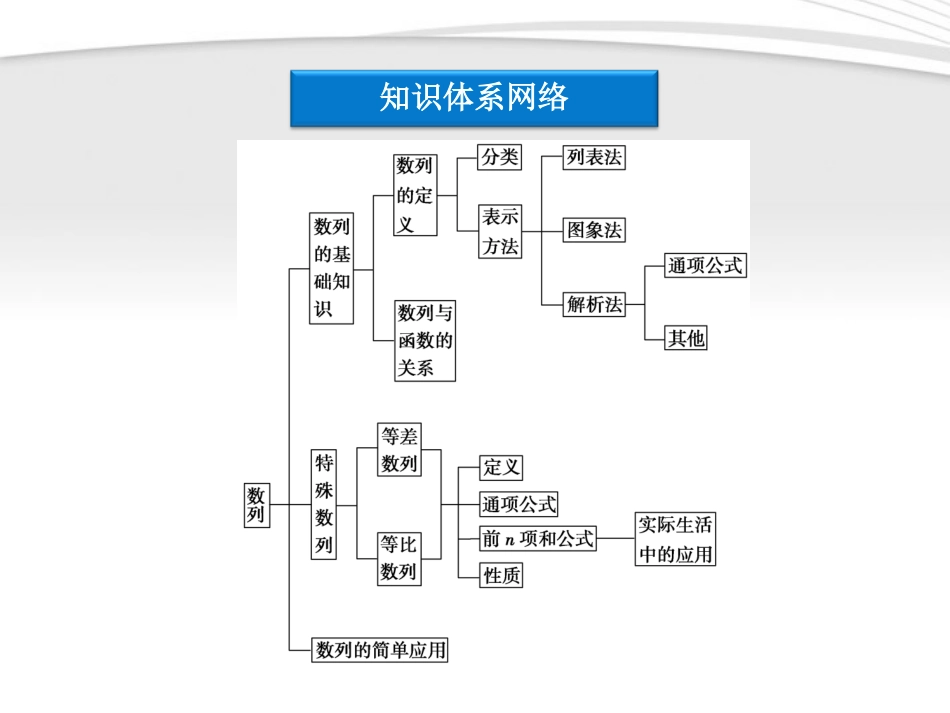
本章优化总结专题探究精讲本章优化总结知识体系网络知识体系网络专题探究精讲数列通项公式的求法题型特点：数列的通项公式是数列的核心内容，它如同函数中的解析式一样，有了解析式便可研究其性质等，而有了数列的通项公式便可研究数列其它问题，求数列通项公式常见题型为：已知数列的前几项，已知数列的前n项和，已知数列的递推关系等条件来求数列的通项公式，题型多为解答题．知识方法：在解题时，根据题目所给条件的不同，可以采用不同的方法求数列的通项公式，常见方法有如下几种：1．观察归纳法观察归纳法就是观察数列特征，找出各项共同的构成规律，横向看各项之间的关系，纵向看各项与项数n的内在联系，从而归纳出数列的通项公式．根据以下数列的前4项写出数列的一个通项公式．(1)12×4，13×5，14×6，15×7；(2)－3,7，－15,31；(3)2,6,2,6.例例11【解】(1)均是分式且分子均为1，分母均是两因数的积，第一个因数是项数加上1，第二个因数比第一个因数大2，∴an＝1n＋1n＋3.(2)正负相间，可用(－1)n来表示符号，各项的绝对值恰是2的整数次幂减1，∴an＝(－1)n(2n＋1－1)．(3)这样的摆动数列，一般求两数的平均数2＋62＝4，而2＝4－2,6＝4＋2，中间符号用(－1)n来表示．an＝4＋(－1)n·2或an＝2，n是奇数6，n是偶数.2．公式法等差数列与等比数列是两种常见且重要的数列，所谓公式法就是先分析后项与前项的差或比是否符合等差、等比数列的定义，然后用等差、等比数列的通项公式表示它．已知数列{an}为无穷数列，若an－1＋an＋1＝2an(n≥2且n∈N*)，且a2＝4，a6＝8，求通项an.例例22【解】 an－1＋an＋1＝2an，∴an－1，an，an＋1成等差数列．又 n≥2且n∈N*，∴数列{an}为等差数列，设首项为a1，公差为d，由a2＝4，a6＝8，可得a1＝3，d＝1，∴通项an＝3＋(n－1)×1＝n＋2.3．利用an与Sn的关系前n项和关系式有两种形式：一种是Sn与n的关系式，记为Sn＝f(n)，它可由公式an＝S1n＝1Sn－Sn－1n≥2直接求出通项an，但要注意n＝1与n≥2两种情况能否统一；另一种是Sn与an的关系式，记为f(an，Sn)＝0，求它的通项公式an已知数列{an}满足关系式lg(1＋a1＋a2＋…＋an)＝n(n∈N*)，求数列{an}的通项公式．【解】由题意知lg(Sn＋1)＝n，∴Sn＝10n－1.当n＝1时，a1＝S1＝9.当n≥2时，an＝Sn－Sn－1＝(10n－1)－(10n－1－1)＝9×10n－1.显然，n＝1时也满足关系式9×10n－1.综上，an＝9×10n－1(n∈N*)．例例334．叠加法、叠乘法有些数列，虽然不是等差数列或等比数列，但是它的后项与前项的差或商具有一定的规律性．这时，可考虑利用叠加或叠乘法，结合等差、等比数列的知识解决．已知a1＝1，an＋1an＝n＋2n，求an.例例44【解】当n≥2时，an＝a1·a2a1·a3a2·…·anan－1＝1×31×42×53×…×n＋1n－1＝nn＋12.而a1＝1也适合上式．故{an}的通项公式an＝12n(n＋1)．已知数列{an}中，a1＝1，且an＋1－an＝3n－n，求数列{an}的通项公式．例例55【解】由an＋1－an＝3n－n，得an－an－1＝3n－1－(n－1)，an－1－an－2＝3n－2－(n－2)，…a3－a2＝32－2，a2－a1＝3－1.当n≥2时，以上(n－1)个等式两端分别相加，得(an－an－1)＋(an－1－an－2)＋…＋(a2－a1)＝3n－1＋3n－2＋…＋3－[(n－1)＋(n－2)＋…＋1]，即an－a1＝31－3n－11－3－nn－12.又 a1＝1，∴an＝12×3n－nn－12－12.显然a1＝1也适合上式，∴{an}的通项公式为an＝12×3n－nn－12－12.5．构造法形如：已知a1，an＋1＝pan＋q(p、q为常数)形式均可用构造等比数列法，即an＋1＋x＝p(an＋x)，{an＋x}为等比数列，或an＋2－an＋1＝p(an＋1－an)，{an＋1－an}为等比数列．已知f(x)＝(x－1)2，g(x)＝10(x－1)，数列{an}满足a1＝2，(an＋1－an)g(an)＋f(an)＝0，bn＝910(n＋2)·(an－1)．求证：数列{an－1}是等比数列．例例66【证明】 (an＋1－an)g(an)＋f(an)＝0，f(an)＝(an－1)2，g(an)＝10(an－1)．∴(an＋1－an)×10(an－1)＋(an－1)2＝0.即(an－1)(10an＋1－9an－1)＝0.又a1＝2，可知对任意n∈N＋，an－1≠0，所以an＋1＝910an＋110. an＋1－1an－1＝910an＋110－1...