高中数学 311实数指数幂及其运算 课件 新人教A版必修1 课件VIP免费

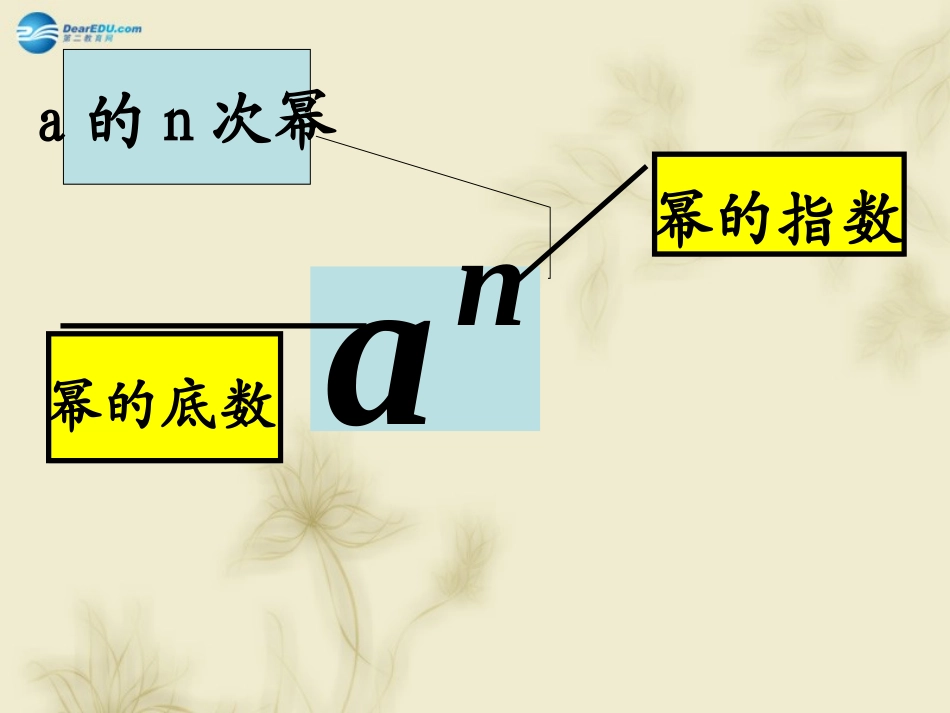
na幂的指数幂的底数a的n次幂整数指数幂概念)(*Nnaaa0anana1na1整数指数幂运算性质),(Znmanm),(Znmanm)(Znbannnmaanab)(nma)(一般地,如果一个数的n次方等于a),,1(*Nnn且那么这个数叫做a的n次方根.axn那么x叫做a的n次方根,其中.,1*Nnn且就是说,如果求a的n次方根，叫做把a开n次方，称作开方运算．?44,)2(4,2122的平方根是）（的立方根是？的立方根是？，，）（888282233总结思考它们之间的个？正数的偶次方根有关系是什么？几2互为相反数个？正数的奇次方根有几1个？负数的奇次方根有1几3.根式的运算性质*),1()(Nnnaann且(1)(2)nnaa当n为奇数时|a|当n为偶数时.１.正数的分数指数幂的意义)1,,,0(*nNnmaaanmnm且２.规定(１))1,,,0(1*nNnmaaanmnm且(２)０的正分数指数幂等于０.(３)０的负分数指数幂无意义.３.有理指数幂的运算性质(１)(２)(３)),,,0(Qsraaaasrsr),,,0()(Qsraaarssr).,0,0(Qrbabaabrrr例１.求下列各式的值(１)(２)(３)(４);)8(33;)10(2;)3(44).()(2baba例２比较5,311,6123的大小.解:,12555663,12111116623又,125123121666125123121故36111235例3.)8116(,)41(,100,84332132求下列各数的值解:422)2(8232332332101)10(1100110021221216422)2()41(6)3()2(323827)32()32()8116(3)43(443例4用分数指数幂的形式表示下列各式(式中a>0):aaaaaa.3.2.1323225212212aaaa311323323aaaa4321232121)()(aaaa、化简下列各式例5)yx65)(yx41(yx5)1(6131211213261y2421211mm2mm)2(2121mm、化简下列各式例6842222)1(4432733)2(yx3xy3)3(23633)b125a8()4(