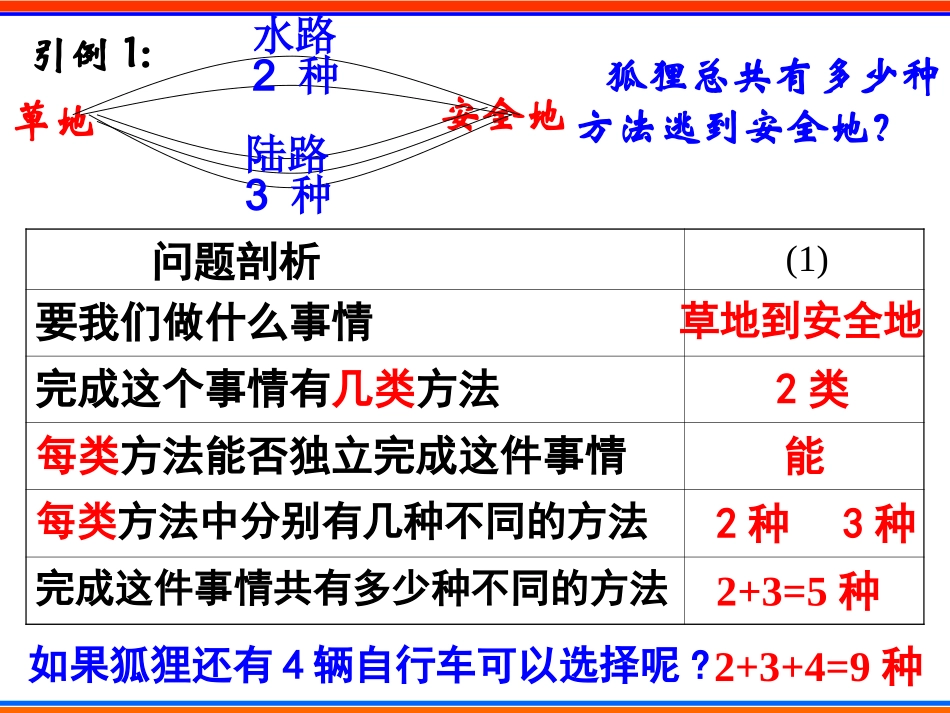
第一章计数原理1.1分类加法计数原理与分步乘法计数原理狐狸想从草地逃到小岛,可以走水路,也可以走陆路,走水路有2艘船,走陆路有3辆车子,问:乘坐这些交通工具,一共有多少种不同的方法,可以从草地逃回到小岛安全地引例1:草地狐狸总共有多少种方法逃到安全地?问题剖析(1)要我们做什么事情完成这个事情有几类方法每类方法能否独立完成这件事情每类方法中分别有几种不同的方法完成这件事情共有多少种不同的方法草地到安全地2类能2种3种2+3=5种水路2种陆路3种如果狐狸还有4辆自行车可以选择呢?2+3+4=9种一、分类加法计数原理完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法.那么完成这件事共有N=m+n种不同的方法.1.1分类加法计数原理与分步乘法计数原理例1:书架的第一层有6本不同的数学书,第二层有7本不同的英语书,第三层有10本不同的语文书,现想从书架上取一本书,共有多少种不同的方法?加问:若第四层中还有8本不同的物理书,第五层中还有9本不同的生物书,又会如何呢?从书架上拿一本书有三类方法能6种,7种,10种6+7+10=23种40种问题剖析(1)要我们做什么事情完成这个事情有几类方法每类方法能否独立完成这件事情每类方法中分别有几种不同的方法完成这件事情共有多少种不同的方法1.1分类加法计数原理与分步乘法计数原理一般归纳:完成一件事情,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法……在第n类办法中有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法.分类加法计数原理狐狸有一共有多少种不同的方法,可以从小岛逃回到自己的房子(安全地)1.1分类加法计数原理与分步乘法计数原理狐狸有一共有多少种不同的方法,可以从草地逃回到自己的房子(安全地)1.1分类加法计数原理与分步乘法计数原理引例2:草地5种方法小岛安全地2种方法问题剖析(2)要我们做什么事情完成这个事情要分几步每步方法能否独立完成这件事情每步方法中分别有几种不同的方法完成这件事情共有多少种不同的方法草地到安全地2步不能5种2种5×2=10种a1a2a3a4a5b1b21.1分类加法计数原理与分步乘法计数原理1.1分类加法计数原理与分步乘法计数原理问题剖析(1)(2)要我们做什么事情草地到小岛草地到房子完成这个事情有几类(步)方法2类2步每类(步)方法能否独立完成这件事情能不能每类(步)方法中分别有几种不同的方法2种,3种5种,2种完成这件事情共有多少种不同的方法2+3=55×2=101.1分类加法计数原理与分步乘法计数原理二、分步乘法计数原理完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有种n不同的方法。那么完成这件事共有N=m×n种不同的方法.例2:书架的第一层有6本不同的数学书,第二层有7本不同的英语书,第三层有10本不同的语文书,现从书架第一层、第二层、第三层各取一本书,共有多少种不同的方法?解:从书架1,2,3层各取一本,可以分成三个步骤完成:第一步从第1层取1本数学书,有6种方法,第二步从第2层取1本英语书,有7种方法,第三步从第3层取1本语文书,有10种方法,根据分步计数原理,得不同的取法有:N=m1×m2×m3=6×7×10=420答:从书架的第1,2,3层个取一本书,有420种不同的方法1.1分类加法计数原理与分步乘法计数原理1.1分类加法计数原理与分步乘法计数原理完成一件事情,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的法,……做第n步有mn种不同的方法,那么完成这件事情有N=m1×m2×…×mn种不同的方法.分步乘法计数原理原理的联系、区别及特点:原理的联系、区别及特点:分类法:相互独立,每种方法均能独立完成这件事分步法:各步骤中的方法相互依存,只有各个步骤都完成才算完成这件事:都要有一个确定的标准,分类时要彻底,无交叉,分步时要恰到好处。:都是有关做一件事情的不同方法的种数的问题。联系联系区别区别特点特点1.1分类加法计数原理与分步乘法计数原理分类加法计数原理与分步乘法计数原理1.1分类加法计数原理与分步乘法计数原理相互联系,分步到达。相互独立,直达目的。分类加法计数原理分步乘法计数原理1.1分类加法计数原理与分...