高中数学 2.4平面向量数量积课件 新人教版必修4 课件VIP免费

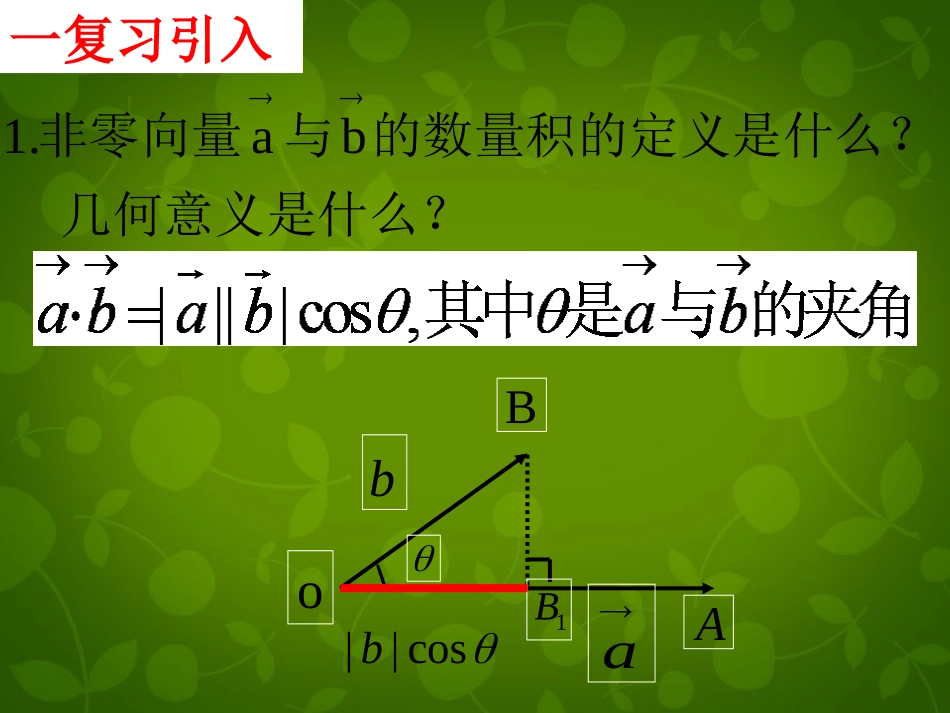
一复习引入1.ab非零向量与的数量积的定义是什么？几何意义是什么？||cosb1BoBAba2.平面向量的数量积满足的运算律？（1）a·b＝b·a；（2）(λa)·b＝λ(a·b)＝a·(λb)；（3）(a＋b)·c＝a·c＋b·c；3.设向量a与b都是非零向量，则平面向量的表示方法有几何法和坐标法，向量的坐标表示，对向量的加、减、数乘运算带来了很大的方便.若已知向量a与b的坐标，则其数量积是唯一确定的，因此，如何用坐标表示向量的数量积就成为我们需要研究的课题.探究（一）：平面向量数量积的坐标表示oxyabijii1jjij101122,axiyjbxiyj则:已知两个非零向量a=(x1,y1),b=(x2,y2),怎样用a与b的坐标表示a·b?1122()()abxiyjxiyj2212122112xxixyijxyijyyj221,0,1iijj因为1212abxxyy所以两个向量的数量积等于它们对应坐标的乘积的和.练习1：已知向量(3,1),a求:(1)(2)13-b=(1,-2)探究（二）：向量的模和夹角的坐标表示(1)向量的模设(,),axy则22222,axyaxy或2aaaaaa或；(2)设1122,)(,),AxyBxy（、222121))xxyy（（则AB�（3）平行（4）垂直0babaab12120xxyy11221221,),(,),//0,(0)axybxyabxyxyb（设则设1122(,),(,),(0,0)axybxyab则11221221,),(,),//0,(0)axybxyabxyxyb（设则(5)设是两个非零向量，其夹角为θ，若那么cosθ如何用坐标表示？,ab1122(,),(,)axybxy121222221122xxyyxyxy例题讲解例1：设a=(5,-7),b=(-6,-4),求a·b及a、b间的夹角θ(精确到1°)解a·b=5×(-6)+(-7)×(-4)=-30+28=-2,747522a524622b03.052742cos926.1rad例2：已知向量(1,2),(,1).abx22abab与平行（1）当时,求x?(2)22abab若与垂直，则7(12)(2)430,2xx得x=-2或22abab与垂直（2）当时,求x?2(12,4),2(2,3)abxabx解：(1)22abab若与平行，则13(12)4(2)0,2xxx得(1)(1,3),(1,1),,cosabab例3已知与的夹角求62cos.4abab变式：已知向量a＝(λ，－2)，b＝(－3，5)，若向量a与b的夹角为钝角，求λ的取值范围.例4已知A(1，2)，B(2，3)，C(-2，5)，试判断ABC的形状，并给出证明.A(1,2)B(2,3)C(-2,5)x0y.ABC是直角三角形)1,1()23,12(AB:证明)3,3()25,12(AC031)3(1ACABACAB思考：还有其他证明方法吗？向量的数量积是否为零,是判断相应的两条线段或直线是否垂直的重要方法之一向量的数量积是否为零,是判断相应的两条线段或直线是否垂直的重要方法之一90,C�变式:已知ABC为直角三角形，AB=(1,3),AC=(2,k),求k值？90(C�解：若，则CACB,CACB=0,-21)+(-k)(3-k)=0,k=1或2.练习已知i=(1,0),j=(0,1),与2i+j垂直的向量是[]A.2i-jB.i-2jC.2i+jD.i+2j已知a=(λ,2),b=(-3,5),且a和b的夹角是钝角,则λ的范围是[]310.310.310.310.DCBABA练习][,10,2,12范围为的取值则若已知mmmaaB1,,-1-.2,2.1,1.1,1.DCBA的夹角是多少？与则已知baba,13,13,3,1练习分析：为求a与b夹角，需先求a·b及|a||b|，再结合夹角θ的范围确定其值.0≤θ≤π13,13,3,1ba解413313ba22,2ba记a与b的夹角为θ22cosbaba又0≤θ≤π4知三角形函数值求角时,应注重角的范围的确定已知a＝(３,４),b＝(４,３),求x，y的值使(xa+yb)⊥a,且｜xa+yb｜=1.753524753524yxyx和练习小结)()(2211jyixjyixba2121yyxx.,22222121yxbyxaA、B两点间的距离公式:已知),,(11yxA),,(22yxB,)()(212212yyxxAB小结2.向量的坐标运算沟通了向量与解析几何的内在联系，解析几何中与角度、距离、平行、垂直有关的问题，可以考虑用向量方法来解决.02121yyxxba0//1221yxyxba222221212121cosyxyxyyxx作业课本第121页习题2.4A组题6,7,8