高二数学应用空间向量解立体几何之用平面法向量求空间距离课件VIP免费

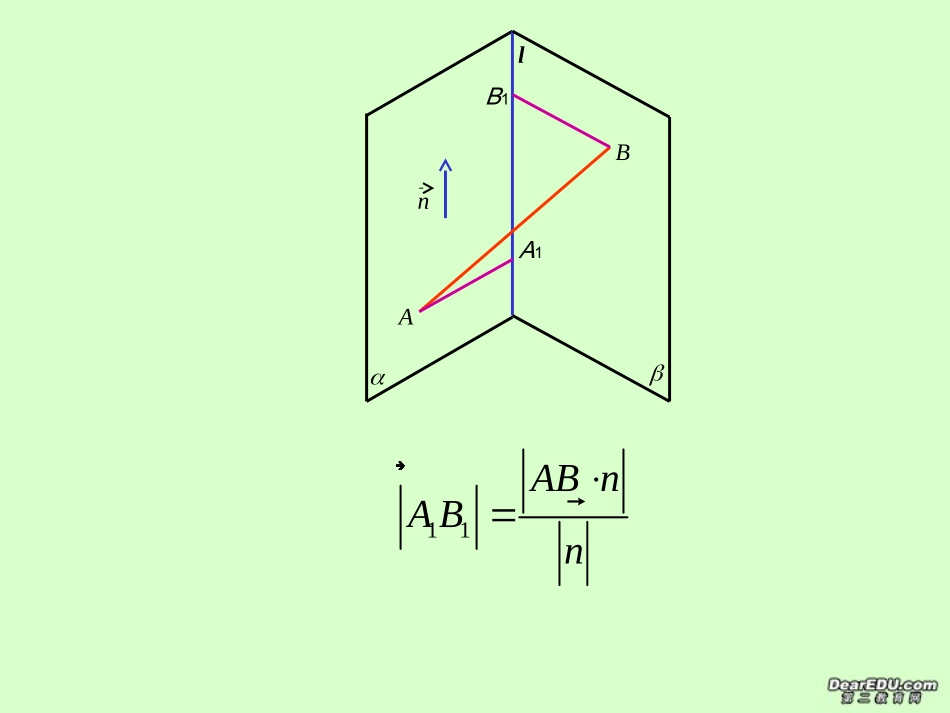
应用空间向量解立体几何之用平面法向量求空间距离甘泉中学李正鹏课本P33已知向量ABa�和轴l，e是l上与l同方向的单位向量.作点A在l上的射影A1，作点B在l上的射影B1，则A1B1叫做向量AB�在轴上或在e方向上的正射影，简称射影.lABB1A1n11ABnABn��课本P42如果表示向量a的有向线段所在直线垂直于平面，则称这个向量垂直于平面，记作a⊥.如果a⊥，那么向量a叫做平面的法向量.la方法指导：怎样求平面法向量？一般根据平面法向量的定义推导出平面的法向量，进而就可以利用平面的法向量解决相关立体几何问题。推导平面法向量的方法如下：例1、在棱长为1的正方体中，求平面的法向量。1111ABCDABCD1ACDABCDxyA1B1C1D1z图1BAMNnABndn�ab一、求异面直线的距离nabAB方法指导:①作直线a、b的方向向量a、b，求a、b的法向量n，即此异面直线a、b的公垂线的方向向量；②在直线a、b上各取一点A、B，作向量AB；③求向量AB在n上的射影d，则异面直线a、b间的距离为例2：已知正方体ABCD-A1B1C1D1的棱长为1，求异面直线DA1与AC的距离。ABDCA1B1C1D1xyz练习:如图,的距离。与，求距离为的到面，点所成的角为面与，且面是正方形，SDACABCDSABCDSAABCDSBABCD145ASCDBxyz例3、已知正方形ABCD的边长为4，CG⊥平面ABCD，CG=2,E、F分别是AB、AD的中点，求点B到平面GEF的距离。DABCGFEnPAOMNPAndn�方法指导：若点P为平面α外一点，点A为平面α内任一点，平面的法向量为n，则点P到平面α的距离公式为二、求点到平面的距离例3、已知正方形ABCD的边长为4，CG⊥平面ABCD，CG=2,E、F分别是AB、AD的中点，求点B到平面GEF的距离。DABCGFExyz练习:的距离。到平面求，，，平面SCDAaADaBCABSAABCDABABCDSA,290SBCDAxyz例4、已知正方形ABCD的边长为4，CG⊥平面ABCD，CG=2,E、F分别是AB、AD的中点，求直线BD到平面GEF的距离。DABCGFExyznnPAd三、求直线与平面间距离小结：1、怎样利用向量求距离？①点到平面的距离：连结该点与平面上任意一点的向量在平面定向法向量上的射影（如果不知道判断方向，可取其射影的绝对值）。②点到直线的距离：求出垂线段的向量的模。③直线到平面的距离：可以转化为点到平面的距离。④平行平面间的距离：转化为直线到平面的距离、点到平面的距离。⑤异面直线间的距离：转化为直线到平面的距离、点到平面的距离。也可运用闭合曲线求公垂线向量的模或共线向量定理和公垂线段定义求出公垂线段向量的模。结论1点P到平面的距离可以通过，在平面内任取一点A，求向量PA�在平面的法向量n上的投影来解决.nPAOMNPAndn�结论2异面直线间的距离可以通过，在两条直线上任意各取一点A、B，求向量AB�在公共法向量n上的投影来解决.BAMNnABndn�ab例5、在边长为1的正方体ABCD-A1B1C1D1中，M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点，求平面AMN与平面EFDB的距离。ABCDA1B1C1D1MNEFxyznnPAd四、求平面与平面间距离