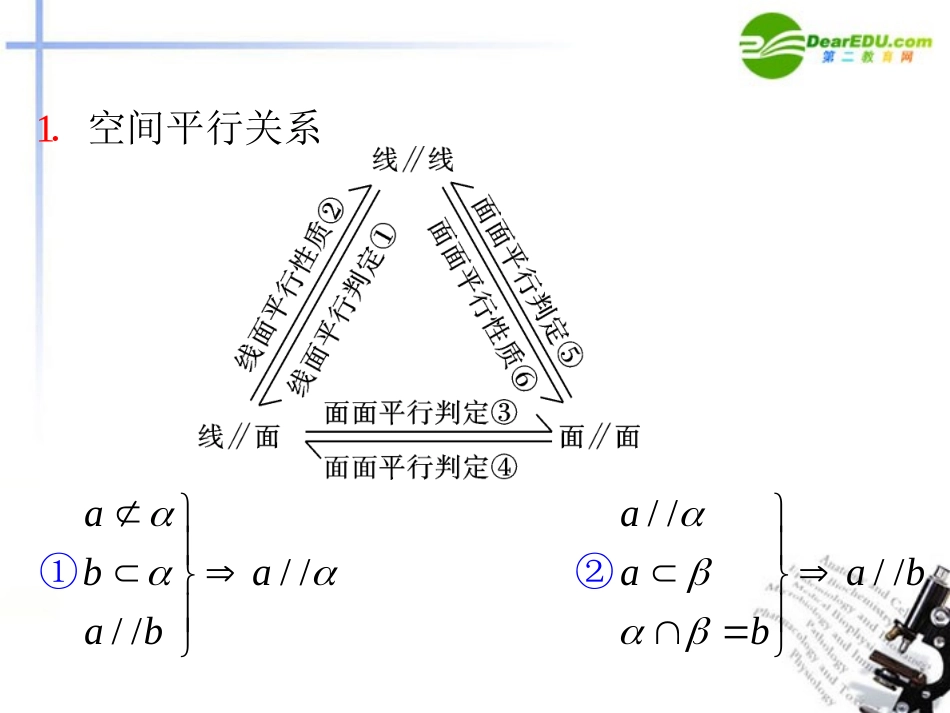
专题四立体几何与空间量/////1///aabaaababb空间平行关系②①.//,////////,//,////,,,//,//,ababAaabambnabmnaaababAmnBb③④⑤⑥2,abacaaabbcbbcO空间②垂.①直关系,,,alaaaalalbcaabbcOalabacb③④⑤⑥【例1】若m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题中为真命题的是()A.若m⊂β,α⊥β,则m⊥αB.若α∩γ=m,β∩γ=n,m//n,则α//βC.若α⊥γ,α⊥β,则β//γD.若m⊥β,m//α,则α⊥β本题主要考查空间中线线、线面、面面的位置关系,可以依据具体的模型(如正方体),对命题的真假作出判断.结合具体的模型,或画出几何图形,容易判断A、B、C是假命题,故选D.D解决此类问题一般用排除法,借助具体的几何模型,并且让模型中的直线和平面“动一动、移一移”举出反例,从而得出正确的结论.【变式训练】(2010·山东卷)在空间中,下列命题正确的是()A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行D由空间直线与平面的位置关系及线面垂直、平行的判定与性质定理可知D正确.【例2】(2010·北京卷)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF//AC,AB=,CE=EF=1.(1)求证:AF//平面BDE;(2)求证:CF⊥平面BDE.证明线面平行(垂直)需转化为证明线线平行(线线垂直).2(1)设AC与BD相交于点G.因为EF∥AG,且EF=1,AG=AC=1,所以四边形AGEF为平行四边形,所以AF∥EG.因为EG⊂平面BDE,AF⊄平面BDE,所以AF∥平面BDE.(2)连接FG.因为EF∥CG,EF=CG=1,且CE=1,所以平行四边形CEFG为菱形,所以CF⊥EG.因为四边形ABCD为正方形,所以BD⊥AC.又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,所以BD⊥平面ACEF,所以CF⊥BD.又BD∩EG=G,所以CF⊥平面BDE.121.证明线面平行的常用方法:(1)由线线平行证明线面平行;(2)由面面平行证明线面平行.2.证明面面垂直的常用方法:(1)由线面垂直证明面面垂直;(2)证明所成二面角为直角.【变式训练】如图所示,在矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.求证:(1)AE∥平面BFD;(2)AE⊥平面BCE.(1)由题意可得,G是AC的中点,连结FG.因为BF⊥平面ACE,则CE⊥BF.又BC=BE,所以F是EC的中点.在△AEC中,FG∥AE.又FG⊂平面BFD,AE⊄平面BFD,所以AE∥平面BFD.(2)因为AD⊥平面ABE,AD∥BC,所以BC⊥平面ABE,则AE⊥BC.又因为BF⊥平面ACE,则AE⊥BF,BC∩BF=B,所以AE⊥平面BCE.【例3】(2010·福建卷)如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点(点E与B1不重合),且EH∥A1D1.过EH的平面与棱BB1、CC1相交,交点分别为F、G.(1)证明:AD∥平面EFGH;(2)设AB=2AA1=2a,在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P.当点E、F分别在棱A1B1,B1B上运动且满足EF=a时,求P的最小值.(1)证线面平行转化为证直线与平面内的一直线平行;(2)求概率的最小值可转化为体积之比,然后应用基本不等式求解(1)在长方体ABCD-A1B1C1D1中,AD∥A1D1.又因为EH∥A1D1,所以AD∥EH.因为AD⊄平面EFGH,所以AD∥平面EFGH.(2)设BC=b,则长方体ABCD-A1B1C1D1的体积V=AB·AD·AA1=2a2b.几何体EB1F-HC1G的体积V1=(1/2EB1·B1F)·B1C1=b/2EB1·B1F.222112221111112211211.22227411.428278,2.EBBFaEBBFaEBBFEBBFaabVabVPVabEBBFaP因为,所以当且仅当时等号成立.从而,,故当且仅当时等号成立所以,的最小值等于(1)证线面平行的常用方法:①线面平行判定定理;②面面平行的定义.(2)求最值问题先列出等式,应用不等式或函数的单调性解决.【变式训练】如图...