1、当您付费下载文档后，您只拥有了使用权限，并不意味着购买了版权，文档只能用于自身使用，不得用于其他商业用途（如 [转卖]进行直接盈利或[编辑后售卖]进行间接盈利）。2、本站所有内容均由合作方或网友上传，本站不对文档的完整性、权威性及其观点立场正确性做任何保证或承诺！文档内容仅供研究参考，付费前请自行鉴别。3、如文档内容存在违规，或者侵犯商业秘密、侵犯著作权等，请点击“违规举报”。
碎片内容
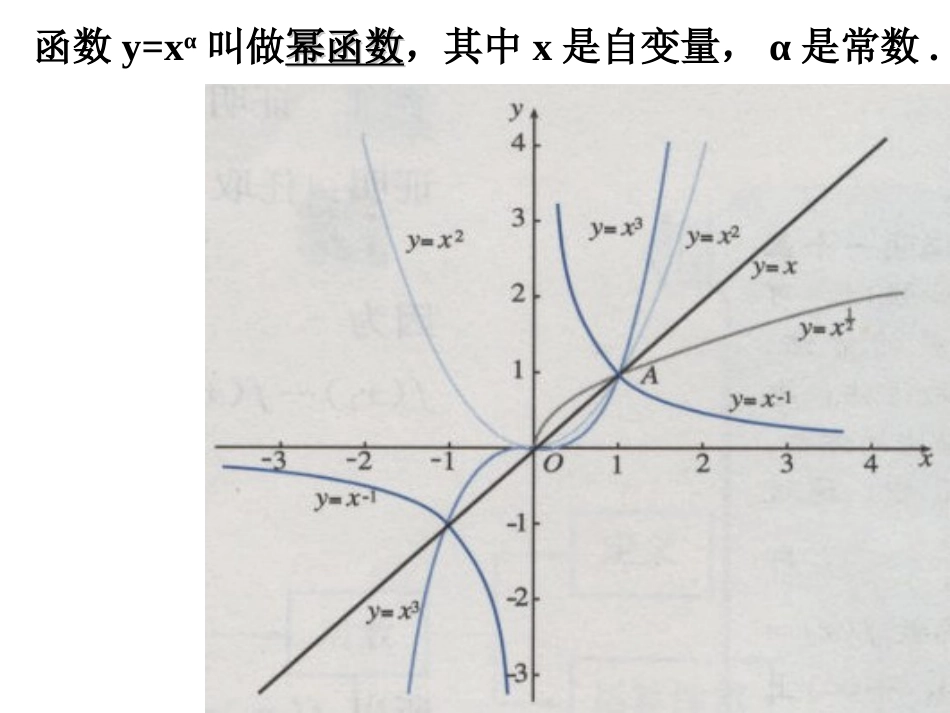
整数指数幂有理指数幂无理指数幂指数对数定义运算性质指数函数对数函数幂函数定义图象与性质定义图象与性质图象性图象性质质对数函数对数函数y=logy=logaax(ax(a＞＞0,0,且且a≠a≠1)1)的图象与性质的图象与性质aa＞＞1010＜＜aa＜＜11定义域定义域:(0,+∞):(0,+∞)值域值域::RR过点过点(1,0),(1,0),即当即当xx＝＝11时时,y,y＝＝00在在(0,+∞)(0,+∞)上是增函上是增函数数在在(0,+∞)(0,+∞)上是减函数上是减函数yyxx00yyxx00(1,0)(1,0)(1,0)(1,0)当x>1时，y>0当x=1时，y=0当00,那么：对数运算性质如下：
从事历史教学，热爱教育，高度负责。
